Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 8

В точке 1 выходной сигнал U₁(t) можно представить в виде суммы основных гармоник с частотами , и нелинейных продуктов, обусловленных первым УП, с частотами _комб , определенными в табл. 9.1:

где N_комб — число комбинационных продуктов определенного вида (см. табл. 9.1).

В точке 2 сигнал не приобретает дополнительных комбинационных составляющих, так как четырехполюсник 1—2 считается линейным. При этом все составляющие сигнала U₁(t) усиливаются в раз и приобретают соответствующий фазовый сдвиг,

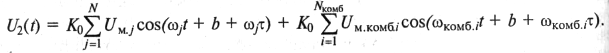
При равномерной диаграмме уровней в линейном тракте, когда уровни сигнала на выходах УП одинаковы, усилитель должен иметь коэффициент усиления равный . Вследствие безынерционности он не должен вносить дополнительных фазовых сдвигов. Тогда в точке 3 получим усиленный в  раз сигнал U₂(t) и, кроме того, нелинейные продукты U'_KOМБ(t), обусловленные нелинейностью второго усилителя и зависящие от уровня основного сигнала на его входе. Нелинейные продукты U'_KOМБ(t) определяются основными гармониками, пришедшими на вход усилителя с дополнительным фазовым сдвигом, равным . Тогда комбинационный продукт второго порядка, созданный вторым усилителем, будет определяться выражением

где  — амплитуда комбинационного продукта,

Для комбинационных продуктов третьего порядка получим аналогично:

Поскольку уровни основных гармоник на выходах первого и второго УП равны, то будут равны и амплитуды соответствующих комбинационных продуктов, возникших в этих УП. Результирующий сигнал U₃(t) на выходе усилителя второго УП будет равен

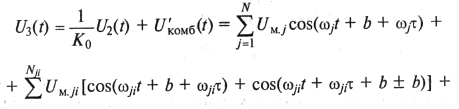
[Paul1]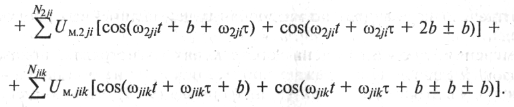 

Здесь , , — число комбинационных продуктов соответствующего вида. Из этого выражения видно, что сложение комбинационных продуктов, образованных в разных УП и пришедших на выход последнего УП (в нашем случае мы ограничились всего двумя УП), происходит по-разному. 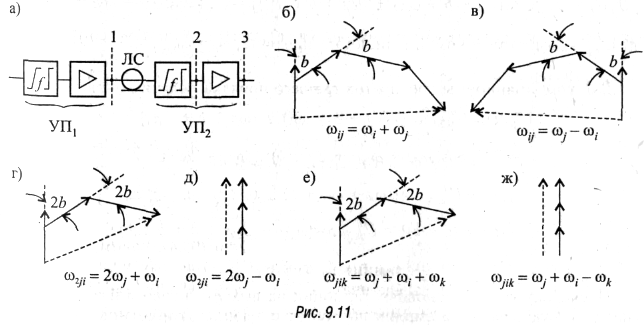Комбинационные продукты второго порядка одной частоты складываются с некоторым фазовым сдвигом  ±Ь, комбинационные продукты третьего порядка — с фазовым сдвигом = b ± b и  = b ± b для соответствующей комбинации. Указанное обстоятельство иллюстрируется рис. 9.11, б, в, г, д, е, ж, где сложение комбинационных продуктов разных УП производится в векторной форме (пунктиром обозначен вектор суммы накопленных нелинейных продуктов). Из рис. 9.11 видно, что наиболее интенсивно происходит накопление нелинейных продуктов вида (2— ) и ( +  — ), для которых фазовый сдвиг между напряжениями нелинейных продуктов, пришедших с разных УП, равен нулю (см. рис. 9.11, д, ж). Такие продукты называются нелинейными продуктами третьего порядка первого рода. Остальные комбинации, для которых сложение напряжений происходит с фазовым сдвигом, отличным от нуля (см. рис. 9.11, б, в, г, е), называются соответственно нелинейными продуктами второго порядка и третьего порядка второго рода.

Нелинейные продукты первого рода складываются алгебраически, т.е. их сумма равна

где n —число УП; , и

соответственно амплитуда напряжения и мощность нелинейного продукта первого рода одного УП. Если диаграмма уровней равномерна, то _i = const = ,  = const =  и

(9.29)

Напряжения нелинейных продуктов второго рода складываются векторно (с учетом фазового сдвига). При таком геометрическом сложении суммарное напряжение нелинейного продукта второго рода  может быть выражено в виде

где  — амплитуда напряжения нелинейного продукта второго рода i-го УП, п — число УП. Учитывая известную зависимость между напряжением и мощностью нелинейного продукта второго рода . Для Равномерной диаграммы уровней, когда  ⁼ const = , получим

(9.30)

Сравнивая (9.29) и (9.30), видим, что накопление мощности нелинейных Продуктов первого рода с увеличением длины линии связи (с увеличением числа УП) происходит значительно интенсивнее, чем нелинейных продуктов второго рода.