Помехи в линейном тракте АСП-ЧРК. Собственные шумы в каналах и трактах ДСП. Общие принципы анализа линейных шумящих цепей, страница 11

Мощность нелинейных продуктов второго порядка, попадающих в полосу пропускания канала связи с граничными частотами F_H, F_B (или нормированными _н и _в), определяется по аналогии с (9.40):

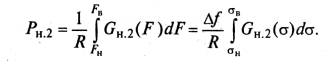
Если (_А — _н) << 1, как, например, для телефонного канала, то можно считать, что для а  [_А, _н] имеем: С _{H 2} ()  G_{H 2}(_k) = const, где  - средняя нормированная частота k-ro телефонного канала в линейном спектре частот. Тогда с учетом (9.37) получим

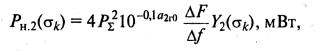(9.43)

где F — полоса пропускания ТЛФ канала, Y₂(_k) — см. (9.42) при  = _k .

Исходя из формул (9.35) и (9.37) найдем спектральную плотность нелинейных продуктов третьего порядка:

Умножим и разделим это выражение на  и учтем, что 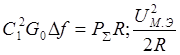=1мВт;

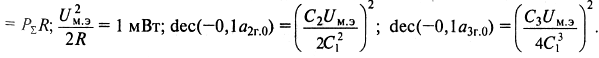
Тогда оно приводится к виду

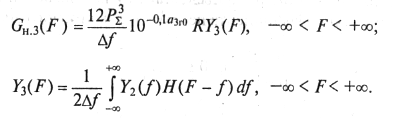(9.44)

Функции G_{H 3}(F) и Y₃(F) — четные. Поэтому, ограничиваясь только положительными частотами (0 < F< +), получим по аналогии с (9.37)

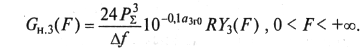(9.45)

Функцию Y₃(F) целесообразно представить в виде Y₃(F)=Y₃₁(F) + Y₃₂(F), где Y₃₁(F) учитывает распределение нелинейных продуктов третьего порядка первого рода (составляющие вида  +  — ), a Y₃₂(F) — третьего порядка второго рода (составляющие вида +  + ). Как и функцию Y₂(f), функцию Y₃(F) целесообразно определять путем графического интегрирования, используя (9.44) и графики Y₂(f) и H(F - f) (рис. 9.16, а, б).

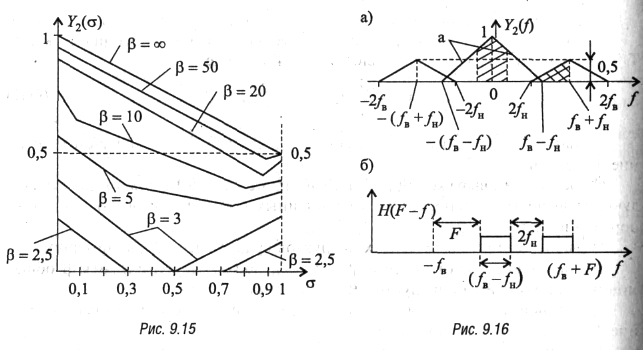
Величина Y₃(F)определяется произведением функции H(F — f) и компонента функции Y₂(f), помеченной буквой а. Численно она пропорциональна, площади фигуры, отмеченной на рис. 9.16, а правой штриховкой. Величина Y₃₂(F) определяется произведением H(F—f) с остальными компонентами функции Y₂(f). Для приведенного на рис. 9.16 примера она будет пропорциональна площади фигуры, заштрихованной левой и правой штриховкой. Примерный вид функций Y₃₁(F) и Y₃₂(F) для F> О показан на рис. 9.17.

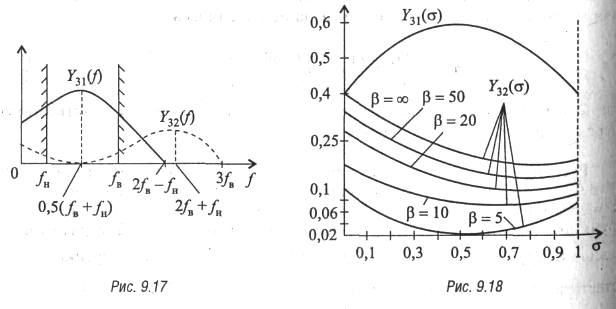
Для нормированной частоты  зависимости Y₃() показаны на рис. 9.18. При этом Y₃₁() определяется выражением

(9.46)

Выражения для Y₃₂() более громоздкие и здесь не приводятся. Мощность нелинейных продуктов третьего порядка в полосе пропускания ТЛФ канала определяется по аналогии с (9.43) в виде

(9.47)

В зависимости от рода нелинейного продукта в (9.47) подставляется значение Y₃₁() или Y₃₂().

На основании выражений (9.42), (9.46) и рис. 9.15, 9.18 можно сделать следующие выводы о распределении нелинейных продуктов второго и третьего порядка в диапазоне 0 < < 1,f_H<F<f_E:

1) распределение нелинейных продуктов существенно неравномерно;

2)  оно зависит от отношения = f_В / f_H, причем с увеличением  общая мощность нелинейных продуктов возрастает;

3) нелинейные продукты третьего порядка первого рода имеют распределение yi\(g), которое не зависит от Р;

4)  мощность нелинейных продуктов на нижних частотах, как правило, выше, чем на верхних.

9.2.4. Влияние перекоса уровней на спектральное распределение нелинейных продуктов

Как указывалось в параграфе 9.1, эффективной мерой повышения защищенности от собственных шумов в верхних каналах является предыскажение уровней передачи. Рассмотрим распределение выходных уровней каналов в линейном спектре некоторого группового сигнала (см. рис. 9.8, в). Вариант 1 соответствует плоскому (или одинаковому) распределению выходных уровней, вариант 2 — распределению при введении «перекоса» уровней или предыскажения уровней. Предыскажение уровней вводится таким образом, чтобы средняя мощность многоканального сигнала не изменилась:

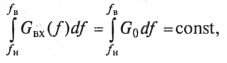(9.48)

где  и G_BX(f) — энергетический спектр входного сигнала соответственно без перекоса и с перекосом уровней.

Рассчитаем спектральное распределение нелинейных продуктов второго и третьего порядка при подаче на вход усилителя многоканального сигнала  энергетическим спектром G_BX(f). Для этого представим G_BX(f) в виде четной Функции частоты/(см. рис. 9.19, а) и по аналогии с рис. 9.12 выразим G_BX(f) в виде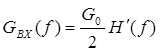, где-<f< + (см. рис. 9.19, б). Здесь функция H соответствует работе без перекоса уровней, в этом случае .Далее используем общие формулы расчета (9.34), (9.35). Из (9.34) получим спектральное распределение нелинейных продуктов второго порядка: