Основные понятия механики деформируемого твердого тела. Общие свойства твердых тел. Внешние силы. Нагрузка, страница 8

Испытания проводятся на специальных испытательных машинах, которые позволяют с высокой точностью фиксировать передаваемую на образец нагрузку. Для определения перемещений и абсолютных величин деформации в образце во время испытаний используют высокоточные приборы – тензометры. Как уже отмечалось, испытания проводятся на стандартных образцах. Для испытаний на растяжение и сжатие в основном используют образцы круглого и прямоугольного поперечных сечений. Длина рабочей части образца, на которой производится измерение перемещений и абсолютных величин деформации, при испытаниях на растяжение обычно принимается равной десяти диаметрам. Длина образца, предназначенного для испытаний на сжатие, не превосходит двух диаметров (при большей длине возможно искривление образца).

В рабочих частях образцов при испытаниях на растяжение и сжатие действуют равномерно распределенные по площади поперечного сечения, соответственно растягивающие или сжимающие напряжения. В силу этого их можно легко определить, разделив величину внутренней силы F на площадь сечения A,

.

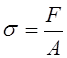С помощью тензометров при определенных величинах нагрузки, которая оказывается равной силе F,  определяются величины удлинения или укорочения Dl участка измеряемой длины образца l. Ввиду того, что образец в своей рабочей части деформируется равномерно на любом участке l, линейные деформации растяжения или сжатия в любой точке рабочей части оказываются одинаковыми и равными величине   e = Dl/l.

В результате испытаний установлено, что при растяжении происходит уменьшение поперечных размеров образца, а при сжатии увеличение. Абсолютная величина отношения поперечной деформации e_попк продольной e_пр носит название коэффициента Пуассона, названного так в честь французского ученого Пуассона:

.

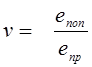Коэффициент Пуассона для различных изотропных материалов находится в пределах от 0 до 0,5.

По результатам испытаний строится диаграмма  растяжения или сжатия, которая в графическом виде изображает зависимость напряжения от величины деформации. На рис. 6 приведена типовая диаграмма растяжения образца из малоуглеродистой стали. На этой диаграмме отмечены характерные точки, так называемые механические характеристики материала: 1–s_пц – предел пропорциональности; 2 – s_у – предел упругости; 3 – s_т – предел текучести; 4 - s_в – предел прочности при растяжении или временное сопротивление.

Рис. 6. Диаграмма растяжения образца из малоуглеродистой стали

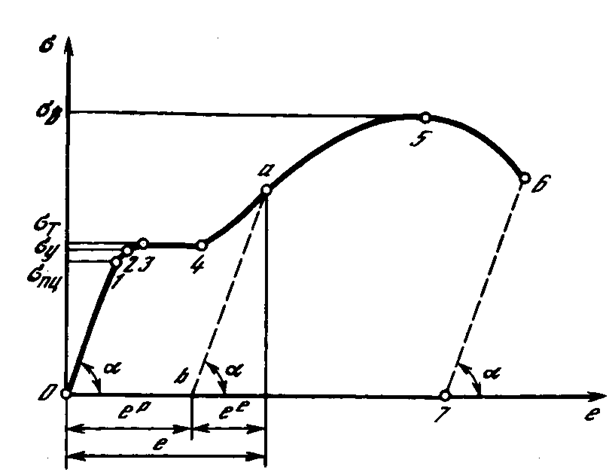На участке  наблюдается линейная зависимость между напряжениями и деформациями , где E – коэффициент пропорциональности, который называется модулем продольной или нормальной упругости (модулем Юнга). Модуль продольной упругости численно равен тангенсу угла наклона первого участка диаграммы 0-1 с осью e (tg a). Приведенная линейная зависимость между напряжениями и деформациями представляет собой закон Гука.

Участок  характеризуется тем, что после снятия нагрузок тело полностью восстанавливает свои размеры и форму. Соответствующие этому участку деформации  называются упругими. Обозначать упругие деформации будем следующим образом: e^e (индекс e от английского слова elasticity – упругость). После снятия нагрузки упругие деформации полностью исчезают. Разница между пределами пропорциональности и упругости обычно невелика и на практике их, как правило, не различают.

Участок s > s_у Характеризуется тем, что после снятия нагрузки тело уже не восстанавливает своих первоначальных размеров и формы, т.е. наблюдается остаточная деформация, которая носит название пластической. Обозначать ее будем e^p (индекс p от английского слова plasticity – пластичность). Полная деформация на этом участке слагается из упругой и пластичной: .