Основные понятия механики деформируемого твердого тела. Общие свойства твердых тел. Внешние силы. Нагрузка, страница 17

где k – постоянная Больцмана, а P – мера вероятности рассматриваемого состояния, определяемая как число возможных микроскопических состояний, отвечающих данному макроскопическому состоянию. Так как практически осуществимые состояния соответствуют наиболее вероятным, то из формулы Больцмана (1.18) следует, что при стремлении изолированной системы к равновесию энтропия возрастает.

Первое и второе начала термодинамики не позволяют определить значение энтропии S₀ при абсолютном нуле температуры . В связи с этим оказывается невозможным теоретический расчет абсолютных значений энтропии, изохорно-изотермного и изобарно-изотермного потенциалов системы, а также константы равновесия. Закон, устранивший указанную трудность, получил название принципа Нернста или третьего начала термодинамики. Однако построение уравнений механики сплошных сред обходится без определения значения энтропии при абсолютном нуле температуры. Поэтому в рамках настоящей работы ограничимся первыми двумя началами термодинамики. Из первого начала термодинамики следует существование функции состояния – полной энергии системы  E_V , а из второго начала термодинамики – существование ещё одной функции состояния: энтропии S_V. Первое начало термодинамики позволяет утверждать, что любое реальное тело и любой его объём  взаимодействуют с окружающей средой через работу, обмен теплом и иными видами энергии. Второе начало термодинамики позволяет учесть влияние температуры тела на его взаимодействие с окружающей средой. Более подробно с основами термодинамики и её использованию в механике сплошных сред можно ознакомиться по книгам А. А. Ильюшина [4] и Л. И. Седова [13].

1.9. Математический аппарат механики сплошных сред

При выводе уравнений механики сплошных сред и механики деформируемого твердого тела, в частности существенные преимущества, дает тензорный аппарат. Тензорная символика, не связанная с определенным выбором системы координат, позволяет произвести доказательство всех теорем и вывод уравнений механики сплошных сред в декартовой прямоугольной системе координат и распространить их на любую криволинейную систему. Более того, в декартовой прямоугольной системе координат исчезает разница между ковариантными и контравариантными величинами, и все дифференциальные операции оказываются полностью идентичными дифференциальному исчислению непрерывных функций, которое изучается в курсе высшей математики. Поэтому изложение механики деформируемого твердого тела в прямоугольной декартовой системе координат тензорным языком оказывается доступным студентам прослушавших курс математического анализа в объеме обычного технического вуза. Достаточно лишь освоить тензорную символику, что не составляет никаких затруднений.

В основе тензорной символики лежат индексные обозначения и соглашение о суммировании по немому повторяющемуся индексу, введенная  А. Энштейном, а также специфическое обозначение производных непрерывной функции. Индексные обозначения вводятся через обозначения координат точки пространства одной буквой с номером оси координат. Например, обозначения x₁, x₂, x₃ определяют координаты точки пространства в ортогональной системе координат Ox₁ x₂ x₃. Тогда проекции вектора a на оси Ox₁, Ox₂, Ox₃ обозначатся как a₁, a₂, a₃. Соглашение о суммировании по немому повторяющемуся индексу в декартовой системе координат состоит в том, что если буквенный индекс повторяется два раза в некотором одночлене, то это означает суммирование всех таких выражений, которые получаются из данного одночлена, когда немой индекс принимает значения 1, 2, 3. Например, выражение u_i v_i представляет собой сумму

.

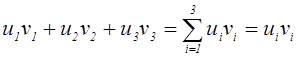Индекс i в этом выражении называется немым потому, что выбор буквы для его обозначения не имеет никакого значения: произведения u_jv_j, u_kv_k и u_iv_i обозначают одно и то же выражение, т.е. u_jv_j = u_kv_k = u_iv_i. Любой индекс в виде латинской буквы в декартовой системе координат пробегает значения 1, 2, 3, т.е. i, j, k, l = 1, 2, 3.