Однако во многих случаях внутреннюю энергию можно считать аддитивной. Так будет для воды, когда не нужно учитывать поверхностное натяжение. Так будет и для упругого тела, подчиняющемуся закону Гука. Если внутренняя энергия аддитивна, то полная энергия произвольного конечного объема V определится следующим образом:
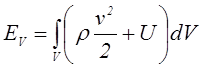. (1.10)
Обозначив через dKV изменение за бесконечно малый промежуток времени dt кинетической, а через dUV внутренней энергии, представим первое начало термодинамики для любого конечного объема в форме:
dKV + dUV = dWV(e) + dWA(e) + dQV(e) + dQ¢V. (1.11)
где dQV(e) – элементарный приток тепла к телу извне, dQ¢V – элементарный приток к телу извне немеханических и нетепловых видов энергии,
dQV = dQV(e) + dQ¢V.
Перейдем к рассмотрению второго начала термодинамики, которое, как и первое начало, представляет собой универсальное утверждение, подтверждаемое всеми известными опытными данными и всеми теоретическими представлениями о механизмах физических явлений. Второе начало термодинамики утверждает, что не возможно устройство, которое переводило бы тепло от тела с меньшей температурой к телу с большей температурой без каких-либо изменений в других телах. Второе начало термодинамики можно еще сформулировать так: нельзя построить вечный двигатель второго ряда, т.е. машину, которая, работая в полном соответствии с первым началом термодинамики по некоторому циклу, периодически совершала бы работу только за счет охлаждения некоторого одного и того же источника тепла с фиксированной температурой. Из второго закона термодинамики следует, что для любого цикла C в термодинамической системе имеет место соотношение:
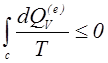(1.12) где T – абсолютная
температура; dQV(e) – приток к системе (к
конечному объему среды) извне тепловой энергии. Знак равенства относится к
обратимым циклам, знак неравенства – к необратимым.
Процесс называется обратимым, если все уравнения для бесконечно малых приращений параметров состояния удовлетворяются также при замене знаков этих приращений на обратные. При обратимом процессе последовательность состояний системы может проходить как в прямом, так и в обратном направлениях. Если процесс не обладает таким свойством, то он называется необратимым. Для обратимых процессов второе начало термодинамики дает
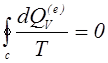(1.13)
Отсюда следует, что величина dQV(e)/T является полным дифференциалом и существует функция состояния SV(m1,…,mn), определяемая соотношением
,
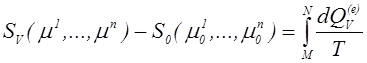(1.14)
где M и N начальная и конечная точки состояния некоторого обратимого процесса. Функция состояния SV носит название энтропии и для обратимых процессов
.
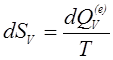(1.15)
На основании (1.14) имеем, что для необратимых процессов
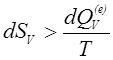
откуда
.
(1.16)
Если ввести в рассмотрение так
называемое некомпенсированное тепло 
, то
неравенство (1.16) можно заменить равенством и в общем случае записать
,
.
(1.17)
Некомпенсированное тепло определяет рассеивание (диссипацию) энергии, которым сопровождаются необратимые процессы. Соотношение (1.17) представляет собой возможную форму записи второго закона термодинамики. При его использовании энтропия определяется с точностью до аддитивной постоянной S0 в начальном состоянии системы. Первое равенство (1.17) называется уравнением баланса энтропии.
Энтропию SV можно ввести статистическим путем. Величина энтропии связывается с вероятностью соответствующего состояния. В статистической физике для энтропии устанавливается следующая формула, принадлежащая Больцману:
,
(1.18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.