Для определения внутренних сил используется так называемый метод сечений. В основу метода сечений положены принцип отвердевания и известные из курса теоретической механики понятия о равновесии тела и принцип Даламбера. Принцип отвердевания состоит в том, что при исследовании равновесия любая мысленно выделенная часть деформируемой среды рассматривается в качестве абсолютно твердого тела. Под равновесием тела понимается его состояние покоя, либо равномерного и прямолинейного движения. Согласно принципу Даламбера действительные силы, воздействующие на механическую систему, в том числе на сплошное тело и его любую часть, уравновешиваются силами инерции. Принцип Даламбера используется в случае приложения к телу динамических сил.
Если к телу приложена статическая нагрузка, то в нагруженном состоянии любая часть тела находится в покое, либо равномерно и прямолинейно движется. Отсюда следует, что все внутренние и внешние силы, действующие на произвольную часть тела, оказываются уравновешенными, т.е. главный вектор и главный момент всей системы сил, которые воздействуют на рассматриваемую часть тела, равны нулю. Это обстоятельство позволяет, составив уравнения равновесия всех сил, действующих на рассматриваемую часть тела, найти зависимость внутренних сил от внешних и в конечном итоге определить внутренние силы. Интересующую часть тела выделяют мысленно проведенными поверхностями и плоскостями. Остальные части тела мысленно отбрасываются, и их воздействие на выделенную часть заменяется внутренними силами. В соответствии с третьим законом Ньютона выделенная часть тела воздействует на отбрасываемую часть через внутренние силы, которые равны по величине и противоположно направлены внутренним силам, действующим на выделенную часть тела.
В случае воздействия на тело динамических сил при составлении равновесия привлекаются силы инерции, приходящиеся на рассматриваемую часть тела, которые на основании принципа Даламбера уравновешивают действующие на эту часть тела все внутренние и внешние силы.
Мысленно выделим из загруженного внешними силами сплошного тела какую-то часть, например, путем рассечения его произвольной поверхностью K, см. рис. 2а. Отброшенную часть тела, заменим внутренними силами. На поверхности сечения выберем какую-нибудь точку P и рассмотрим внутренние силы, приходящиеся на элементарную площадку DA в окрестности этой точки. Ориентация площадки в пространстве определяется нормалью, которую будем считать положительной, если она направлена во внешнюю сторону по отношению к выделенной части тела.
Главный вектор и главный момент внутренних сил, приходящихся на элементарную площадку DA, обозначим соответственно через DF и DM. В общем случае направление главного вектора DF не совпадает с нормалью n к площадке DA. Принимая, что внутренние силы распределены по сечению непрерывным образом, получим, устремив площадь DA к нулю,
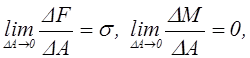 (1.1)
(1.1)
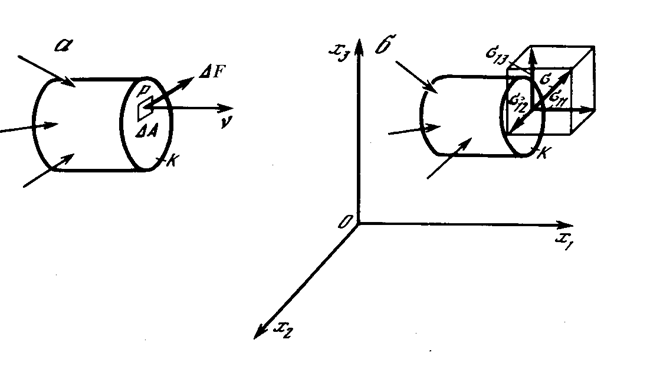
Рис.2. Определение напряжения в точке P сечения K
Предел отношения внутренней силы, действующей на элементарную площадку, площадь которой стремится к нулю, определяет плотность распределения внутренних сил в рассматриваемой точке P по площади сечения, включающей в себя площадку DA. Так определенная плотность внутренних сил называется напряжением s. Таким образом, напряжение в любой точке сплошного тела представляет собой плотность распределения внутренних сил по площади сечения. Напряжение является векторной величиной и имеет размерность силы, деленной на площадь [s] = ML-1T-2. Единицей измерения напряжения является паскаль (Па), который равен ньютону, деленному на метр в квадрате, Н/м2.
В принципе можно предположить, что
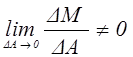
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.