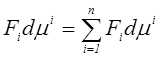Основные понятия механики деформируемого твердого тела. Общие свойства твердых тел. Внешние силы. Нагрузка, страница 15

.

Этим правилом будем пользоваться и в дальнейшем.

Взаимодействие системы с физическими полями осуществляется за счет притока (или оттока) к ней других немеханических видов энергии Q_i. Если через dQ_V обозначить полный приток к системе (конечному объему среды) немеханических видов энергии за бесконечно малое время dt, то по аналогии с (1.2) можно записать

.                                                (1.3)

Приток энергии dQ_V и элементарные работы  и  внешних макроскопических сил не являются в общем случае дифференциалами каких-либо функций.

Рассмотрим процесс, протекающий в пространстве состояний от точки M со значениями параметров состояния  по кривой l₁ до точки N со значениями параметров состояния m ⁱ. Полный приток энергии, который система (конечный объем среды) получают извне, в этом процессе равен

.

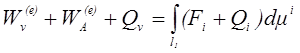Если далее система совершит цикл C, тогда первое начало термодинамики, или закон сохранения энергии, сведется к утверждению, что полный приток энергии, поступающий извне к системе (к конечному объему среды), совершающей любой осуществимый цикл, равен нулю

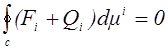  .                                             (1.4)

Первое начало термодинамики можно сформулировать как невозможность осуществления вечного двигателя первого ряда, т.е. циклически работающей машины без использования какого-либо внешнего по отношению к этой машине источника энергии. Это утверждение следует рассматривать как закон, подтверждающийся всеми известными опытными данными.

Из закона сохранения энергии непосредственно следует, что полный приток энергии к системе (к конечному объему среды) не зависит от процесса, а всецело определяется начальным и конечным состояниями системы. Действительно. Пусть цикл состоит из двух процессов, определяемых произвольными кривыми l₁ и –l₂: C = l₁ – l₂. Тогда на основании (1.4) получим

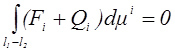
или

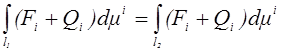                                  (1.5)

Тем самым получено доказательство нашего утверждения о том, что полный приток энергии к системе извне полностью определяется начальным и конечным состояниями системы:

,                     (1.6)

где E_V – функция параметров состояния системы (конечного объема среды), называемая полной энергией системы.

Таким образом, из первого начала термодинамики следует, что существует функция состояния E_V(m ¹,…,m ⁿ), полный дифференциал, который равен сумме элементарных работ внешних макроскопических сил dW_V^(e) и dW_A^(e), а также приложенных внутри объема V и на его поверхности A элементарных притоков к системе (к конечному объему среды) извне других, немеханических, видов энергии dQ_V:

,                                   (1.7)

или

.

Равенство (1.7)  является одной из возможных формулировок первого начала термодинамики. При его использовании полная энергия системы E_V(m¹,…,mⁿ) определяется с точностью до аддитивной постоянной – значения E₀ в начальном состоянии системы. В силу равенства (1.7) величины F_i и Q_i не могут быть произвольными функциями параметров состояния, они должны удовлетворять условиям интегрируемости:

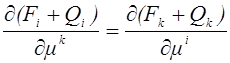.                                        (1.8)

Соотношения (1.8) являются необходимыми и достаточными условиями существования функции E_v(m^1,…,mⁿ), удовлетворяющей равенству (1.7).

Введем плотность кинетической энергии в единице объема rv²/2, где r - массовая плотность, v – скорость, и положим

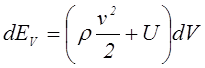.                                           (1.9)

Здесь через V обозначен объем тела, а через U – скалярная функция параметров состояния, называемая плотностью внутренней энергии. Внутренняя энергия U_V, как и полная энергия E_V, определяется с точностью до аддитивной постоянной и существует для каждой термодинамической системы. Полную и внутреннюю энергию можно вводить как для всего тела в целом, так и для отдельных его частей. Внутренняя энергия, в общем случае, не обладает свойством аддитивности, т.е. внутренняя энергия тела в целом не равна сумме внутренних энергий составляющих это тело частей. Так, например, внутренняя энергия одной капли воды не равна сумме внутренних энергий двух мелких капель, из которых она образовалась, если учитывается энергия поверхностного натяжения. Здесь часть энергии затрачивается на изменение температуры.