Основные понятия механики деформируемого твердого тела. Общие свойства твердых тел. Внешние силы. Нагрузка, страница 18

Индекс, который встречается в одночлене один раз, называется свободным. Например, в формуле R_i = w_iju_j индекс i свободный, а jнемой. Свободный индекс присутствует в обеих частях равенства, немой – только в правой части. Свободный индекс, как и немой, пробегает все значения от единицы до трех. R_i обозначает проекцию вектора R на ось Ox_i. Последняя формула в развернутом виде представляет три выражения:

R₁ = w₁₁u₁ + w₁₂u₂ + w₁₃u₃,

R₂ = w₂₁u₁ + w₂₂u₂ + w₂₃u₃,

R₃ = w₃₁u₁ + w₃₂u₂ + w₃₃u_3.

Если u_j = l_jkv_k, то R_i = w_ijl_jkv_k. Здесь индекс i свободный, а j и k немые, по которым производится суммирование от 1 до 3. Эта формула в развернутом виде представляет следующие три выражения:

R₁=w₁₁(l₁₁v₁+l₁₂v₂+l₁₃v₃)+w₁₂(l₂₁v₁+l₂₂v₂+l₂₃v₃)+w₁₃(l₃₁v₁+l₃₂v₂+l₃₃v₃),

R₂=w₂₁(l₁₁v₁+l₁₂v₂+l₁₃v₃)+w₂₂(l₂₁v₁+l₂₂v₂+l₂₃v₃)+w₂₃(l₃₁v₁+l₃₂v₂+l₃₃v₃),

R₃=w₃₁(l₁₁v₁+l₁₂v₂+l₁₃v₃)+w₃₂(l₂₁v₁+l₂₂v₂+l₂₃v₃)+w₃₃(l₃₁v₁+l₃₂v₂+l₃₃v₃).

Отсюда видно, что величина с двумя индексами, независимо от того являются они свободными или немыми, в развернутом виде представляет девять значений. Например, w_ij: w₁₁, w₁₂, w₁₃, w₂₁, w₂₂, w₂₃, w₃₁, w₃₂, w₃₃.

Приведенные примеры показывают, что индексные обозначения вместе с соглашением о суммировании по немому повторяющемуся индексу позволяют одной формулой простого вида представить группу весьма громоздких выражений. Индексная запись, существенно упрощая проводимые выводы каких-либо выражений, придает этим выводам предельно возможную лаконичность и обозримость.

Индексные обозначения вместе с соглашением о суммировании по немым повторяющимся индексам лежат в основе тензорной символики. Существует несколько форм тензорной символики. Мы будем пользоваться одной из наиболее лаконичной и просто заполняющейся, при которой частная производная какой-либо функции по произвольной координате обозначается посредством запятой, следующей за функцией, либо за индексом. Например,

; ; ; .

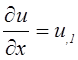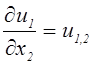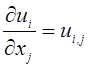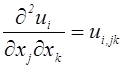В современной литературе по механике сплошных сред широкое распространение находит также применение дифференциального оператора Ñ:

; ; ; .

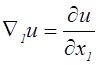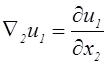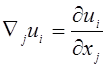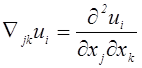После освоения тензорной символики даже те, кто не знаком с тензорным исчислением, окажутся в состоянии понимать материал, изложенный тензорным языком, и естественным образом смогут овладеть тензорным аппаратом в целом. Здесь ограничимся несколькими лишь замечаниями. Тензорное исчисление представляет математический аппарат, с помощью которого формулируются инвариантные, т.е. не зависящие от выбранной системы координат, соотношения между изучаемыми объектами. В координатной системе отсчета тензор представляется своими компонентами, которые в каждой системе имеет свои, отличные от другой системы, значения. Но между значениями компонент тензора в различных системах отсчета существуют вполне определенные зависимости, которые, собственно, и указывают на принадлежность рассматриваемого объекта к тензорам. Это позволяет изучать сложные взаимосвязи между объектами в простейших системах координат, а затем с помощью известных формул перейти к соотношениям в любой другой системе координат. Эти формулы называются тензорным законом преобразования. Так, например, тензорный закон преобразования для компонент тензора второго ранга в ортогональной декартовой системе координат записывается в виде формулы:

P_ij = a_ika_jlp¢_kl,                                              (1.21)

Где p_ij и p^¢_kl – компоненты тензора второго ранга в двух различных координатных системах, связанных преобразованием e_i = a_ije¢_j. Здесь e_i и e¢_j – два ортонормированных базиса рассматриваемых координатных систем.

Имеется большое число учебной литературы, посвященной тензорному исчислению. Достаточный объем сведений о тензорном аппарате для механики сплошных сред содержится в учебнике А. В. Бабкина и В. В. Селиванова.

Вопросы и задачи к первой главе

Что изучает механика деформируемого твердого тела?

Каким образом механика деформируемого твердого тела связана с механикой сплошных сред и физикой?

В чем заключается основное отличие механики деформируемого твердого тела от теоретической механики?

Какими механическими свойствами определяется надежность сооружений и машин?