Основные понятия механики деформируемого твердого тела. Общие свойства твердых тел. Внешние силы. Нагрузка, страница 7

Вектор  называется перемещением точки M¢. Если тело сориентировано в декартовой системе координат, то перемещение точки M¢, т.е. вектор , можно разложить на составляющие, параллельные координатным осям Ox₁, Ox₂ и Ox₃, которые обозначаются соответственно u₁, u₂ и u₃, см. рис. 3.

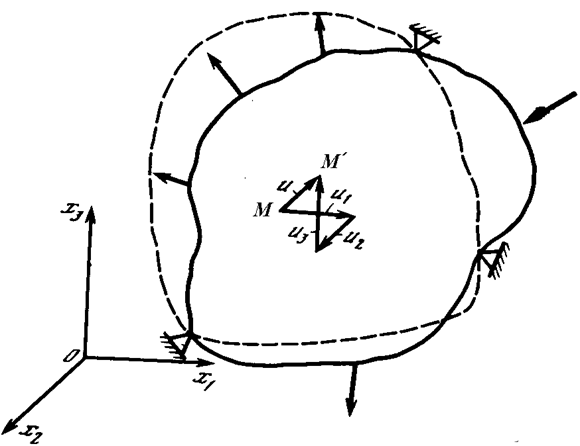
Рис. 3. Перемещение точки Mпри деформации тела

Эти составляющие являются функциями координат точек тела и времени: u_i=u_i (x₁, x₂, x₃,t). Они являются положительными, если направлены в сторону положительных значений координатных осей. Перемещения имеют размерность длины: [u_i] = L. Единицей их измерений является метр (м).

Изменения расстояний между отдельными точками и изменения углов между произвольными лучами в каждой точке тела носят название деформации. Слово деформация имеет двоякий смысл. С одной стороны оно выражает качественное изменение состояния тела, при котором происходит изменение размеров  и формы тела. С другой стороны оно служит количественной мерой изменения геометрических размеров в окрестности точки.

Рассмотрим деформацию тела в окрестности произвольной точки M (рис.4). Пусть до воздействия на тело внешних сил точка M отстоит от близлежащей точки N на расстоянии s. Под воздействием внешних сил точки M и N переместились соответственно в положения M¢ и N¢, причем расстояние между ними изменилось на величину Ds, которую называют абсолютной деформацией.

Величину

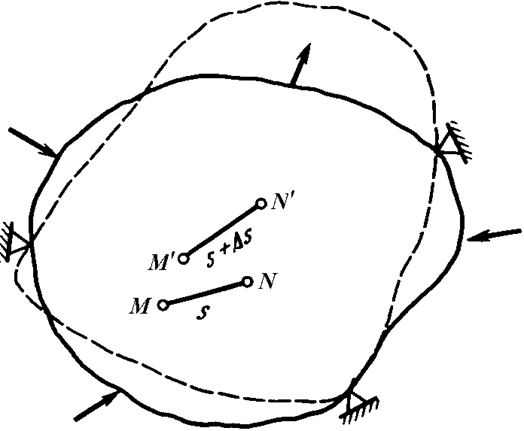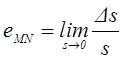
Рис. 4. Деформация тела в окрестности точки Mпо направлению MN

называют линейной деформацией в точке M по направлению MN. В этой же точке M в другом направлении линейная деформация будет другой. Обычно деформации рассматриваются в направлении координатных осей Ox₁, Ox₂ и Ox₃. Тогда величины линейных деформаций в  произвольной точке M обозначаются следующим образом: e₁₁, e₂₂ и e₃₃, где индексы указывают направление линейной деформации. Величина линейной деформации безразмерна, а ее знак зависит  от характера изменения расстояний между исследуемой точкой M  и близлежащей точкой N (Ds). Если это расстояние при внешнем воздействии увеличивается, то линейная деформация считается положительной и носит название деформации растяжения. В противном случае деформация отрицательна и называется она деформацией сжатия.

Кроме линейной деформации вводится понятие угловой деформации. Рассмотрим прямой угол, образованный в произвольной точке M недеформированного тела двумя отрезками MN₁ и MN₂ (рис. 5), где N₁ и N₂ близлежащие к M точки. После нагружения тела внешними силами этот угол изменится и примет значение N¢₁M¢N¢₂.

Приближая неограниченно точки N₁ и N₂ к M, сохранив при этом угол N₁MN₂ прямым, получим в пределе угловую деформацию

.

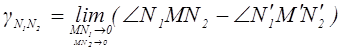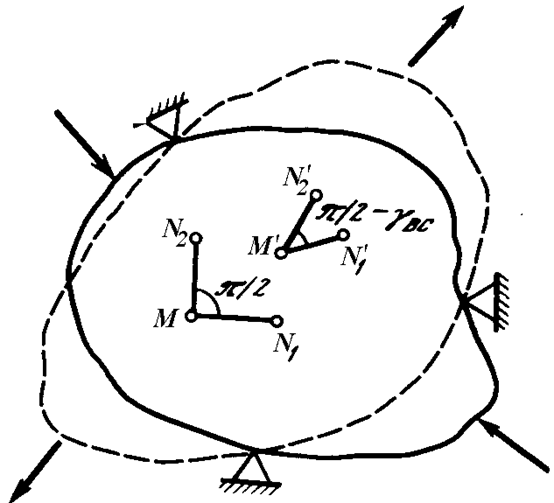Рис. 5. Угловая деформация в точке M плоскости MN₁N₂

Величина  носит название угловой деформации или угла сдвига в точке M плоскости MN₁N₂. В координатных плоскостях углы сдвига обозначаются следующим образом: e₁₂, e₂₃, e₃₁. Углы сдвига измеряются в радианах и считаются положительными в случае, когда при деформации происходит уменьшение прямого угла.

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки образует деформированное состояние в точке.

1.6. Механические свойства материалов

В механике деформированного твердого тела для установления зависимости между напряжениями и деформациями пользуются результатами испытаний определенного типа образцов (стандартных образцов). Основным видом испытаний являются испытания на растяжение и сжатие, при которых в рабочей части образца реализуются только деформации растяжения или сжатия. Для изотропных материалов на основании этих испытаний определяются механические свойства материала при деформациях растяжения, сжатия и сдвига.

Для анизотропных материалов требуются дополнительные испытания на сдвиг, при которых в рабочей части образца реализуются одни лишь деформации сдвига.