Основные принципы практического применения высокопроизводительных нестационарных процессов резания, страница 6

Предложенный способ обработки ступенчатыми резцами с оптимальным распределением припуска между режущими элементами (см. разд. 3.10) реализован в конструкции резца с расположением элементов не в основной (горизонтальной) плоскости (рис. 3.27, 3.25,б; 6.9,а; 6.11), как это принято в традиционно применяемых схемах, а в плоскости, перпендикулярной основной (вертикальной) (см. рис. 6.12). Такая схема расположения режущих элементов позволяет значительно сократить время на обработку, за счет уменьшения хода резца, так как в осевом направлении лезвия резцов смещены относительно друг друга на расстояние 1 - 2 мм. Кроме того, значительно повышается виброустойчивость системы вследствие:

во-первых, наличия “натяга” системы, за счет такого углового расположения резцов, чтобы в моменты входа в контакт и выхода из контакта их лезвий с выступами на заготовке как минимум один резец осуществлял процесс резания;

во-вторых, уменьшения суммарных сил и крутящих моментов.

Проведенный силовой анализ рассматриваемых схем размещения режущих элементов в державке резца подтвердил эти положения.

1.2.1Кинематический анализ схем резания ступенчатыми резцами

Схема действия сил и силовое поле в случае размещения трех режущих элементов в горизонтальной плоскости представлены на рисунке 6.11. При таком расположении режущих элементов суммарные составляющие силы резания, соответственно, равны:

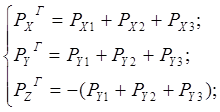                                                                                         (6.1)

 Равнодействующая сил, воздействующих на инструмент, определяется по известной формуле:

.                                                              (6.2)

Из рисунка рис. 6.11,б видно, что вектор Р образует с координатными осями X , Y , Z , соответственно, углы e, w, b. Тогда:

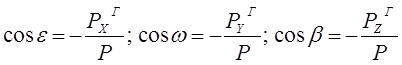                                      (6.3)

Кроме этого, принятая базовая длина резца L должна быть подкорректирована для каждого из режущих элементов на соответствующую ему глубину резания:

для элемента 1:                  l₁ = L + t₁;

для элемента 2:                  l₂ = L + t₁ + t₂;

для элемента 3:    l₂ = L + t₁ + t₂ + t₃.

С учетом указанного, момент, плоскость действия которого совпадает с плоскостью XY , равен:

                                                       (6.4)

Момент, действующий в плоскости ZY:

                                               (6.5)

Суммарный момент сил

                                                                (6.6)

Вектор образует с координатными осями X, Y, Z соответственно углы e`, w`, b`.

Тогда: 

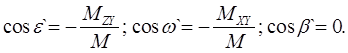                                             (6.7)

Схема действия сил и силовое поле в случае размещения трех режущих элементов в вертикальной плоскости представлены на рисунке 6.12. Суммарные составляющие силы резания в этом случае равны:

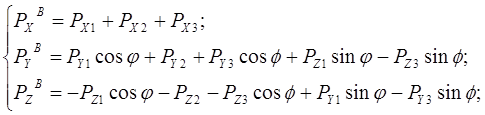.                                (6.8)

Момент, плоскость действия которого совпадает с плоскостью XY, равен:

                      (6.9)

Момент, действующий в плоскости ZY:

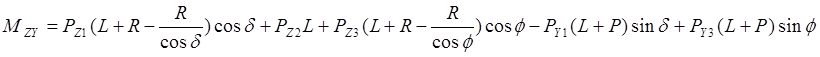 (6.10)

Анализ и сравнение зависимостей (6.1) и (6.8) позволяют сделать следующие заключения.

В первом приближении суммарные осевые составляющие для рассматриваемых случаев размещения режущих элементов равны между собой:

.                                                                                (6.11)

Учитывая то, что значения тригонометрических функций именьше единицы, справедливы зависимости:

                                                                        (6.12)

Таким образом, силовые нагрузки на инструмент при вертикальном расположении режущих элементов меньше, чем при горизонтальном расположении и величина этих нагрузок зависит от углов d и f.

В случае равенства d = f  зависимость (6.8) будет иметь вид:

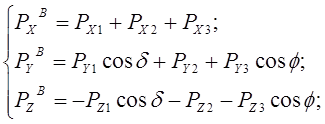.                                                                   (6.13)

В случае, когда d  = f  = 90°, силовые нагрузки будут минимальные: , .

При равенстве d  = f  = 0° силовые нагрузки имеют максимальные значения:

                                                           (6.14)

т.е. наблюдаются те же зависимости, что и в случае горизонтального расположения режущих элементов.

Если принять, что все режущие элементы выполнены из одного материала и условия работы у них близки, то можно принять условие:

 и                                                          (6.15)

Тогда для схемы горизонтального расположения по зависимости (6.1)

 и .                                                                           (6.16)

Для схемы вертикального расположения по зависимости (6.8) при d = f:

                        (6.17)

С целью характеристики и сравнения силовых нагрузок при вертикальной и горизонтальной схемах крепления режущих элементов может быть введен коэффициент изменения силовой нагрузки H_Р:

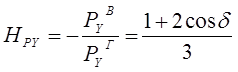                                                                      (6.18)

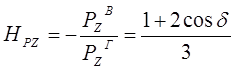                                                                       (6.19)

Выражения (6.18) и (6.19) справедливы при количестве режущих элементов, равном трем. Для большего количества режущих элементов были получены обобщенные зависимости для определения коэффициента изменения силовой нагрузки. При этом считали, что режущие элементы расположены симметрично относительно оси Y. В случае четного числа режущих элементов (n = 2, 4, 6, ...):

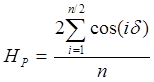.                                                                                                     (6.20)

При нечетном числе режущих элементов (n = 3, 5, 7, ...):

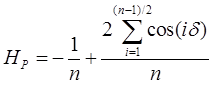.                                                                           (6.21)