1. Преобразование сигналов в нелинейных электрических цепях.
Линейные цепи – это цепи параметры элементов, которых не зависят от величины воздействия. В природе линейных элементов не встречается. Нелинейные цепи – это цепи параметры элементов, которых зависят от величины воздействия. Цепь будет называться нелинейной, если есть хотя бы 1 нелинейный элемент. Параметры не задаются и определяются только характеристиками. Для резистивного элемента это ВАХ i=i(u). Для индуктивности Ампер-Веберная Характеристика ψ=ψ(i). Для емкости Воль-Кулонная Характеристика q=q(u). Наиболее распространенными резистивными элементами являются ламповые и ПП приборы, используемые в радиотехнике для усиления и преобразования сигналов. Важные параметры резистивного элемента статическое и динамическое сопротивление. Статическим сопротивлением называется сопротивление постоянному току.
Rст=u/i=Uo/Io. Rдин=Um/Im=Δu/Δi=dU/dI. Иногда вместо Rдин пользуются понятием динамическая крутизна Sдин=Rдин=dI/dU. Rст – положительно, Rдин – отрицательно на падающих участках ВАХ.
Примером нелинейной индуктивности может быть индуктивность с ферритовым стержнем обтекаемым сильным током доводящим сердечник до состояния насыщения. В состоянии насыщения увеличение тока в индуктивности не вызывает пропорционального увеличения потокосцепления. АВХ принимает нелинейный характер. Примером нелинейной емкости является варикап и вариконд. В нелинейных цепях не выполняется принцип наложения. Невозможно предсказать реакцию цепи при воздействии 2х сигналов, если известны реакции от каждого сигнала в отдельности. i=au2; u1, u2 – воздействующие сигналы; i1=au12, i2=au22, u=u1+u2; i=a(u1+u2)2=au12+au22+2au1u2. Реакция от суммы воздействия отличается от суммы реакции на каждое воздействие в отдельности на величину 2au1u2, которое появляется в случае одновременного воздействия обоих сигналов.
u1=Um1cosωot, u2=Um2cosΩt. i=a(Um1cosωot+Um2cosΩt)2=aUm12cos2ωot+aUm22cos2Ωt+2aUm1Um2cosωotcosΩt =(a/2)Um12+(a/2)Um12cos2ωot+(a/2)Um22+(a/2)Um22cos2Ωt+aUm1Um2cos(ωo-Ω)t+aUm1Um2cos(ωo+Ω)t.
Спектральная диаграмма воздействия на нелинейный элемент.
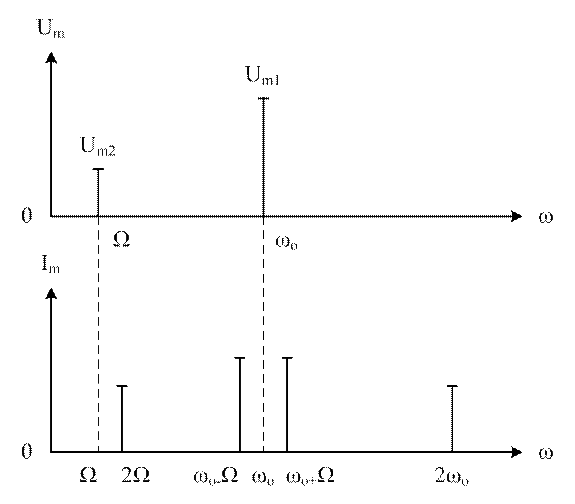
Нелинейный элемент преобразует спектр сигнала. Все спектральные компоненты токов оказались новыми, и их нет в воздействующем напряжении. В этом смысле нелинейные цепи обладают большими возможностями, чем линейные и широко используются для преобразования сигналов путем изменения их спектров.
2. Аппроксимация характеристик нелинейных элементов.
Параметры нелинейных элементов зависят от величины воздействия. Поэтому нелинейные элементы описываются характеристиками. При составлении математического описания работы цепей, содержащих нелинейные элементы необходимо, чтобы их характеристики были представлены аналитически (в виде формул). Под аппроксимацией понимается приближенное аналитическое представление характеристик нелинейного элемента, заданных таблицами и графиками. На практике наибольшее применение находят полиномиальное, кусочно-линейная и аппроксимация трансцендентальными функциями.
1) полиномиальная аппроксимация заключается в том, что зависимость между током и напряжением в нелинейном резистивном элементе представляется в виде полинома n-ой степени. i=ao+a1u+a2u2+...+anun;
ao, a1,..., an – коэффициенты аппроксимации.
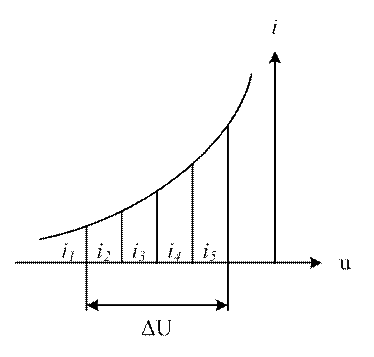
ΔU – интервал аппроксимации определяется возможными изменениями напряжения; Δ – шаг аппроксимации определяет точки на кривой; Δ=ΔU/n; n – степень полинома.
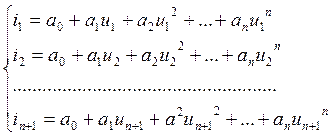
ao÷an – неизвестные коэффициенты.
Чем выше степень полинома, тем точнее аппроксимация, но и тем выше порядок системы. Поэтому ограничивается полиномами невысокой степени:
а) 1й степени, n=1. i=ao+a1u;
б) n=2. i=ao+a1u+a2u2;
в) укороченные полином 3й степени. i=ao+a1u+a2u2+a3u3;
г) укороченные полином 5й степени. i=ao+a1u+a3u3+a5u5;
2) кусочно-линейная заключается в замене плавно меняющейся зависимости i=i(u) к приближенной, состоящей из отрезков линий, выбираемые как касательные к реальной характеристике в нескольких точках.
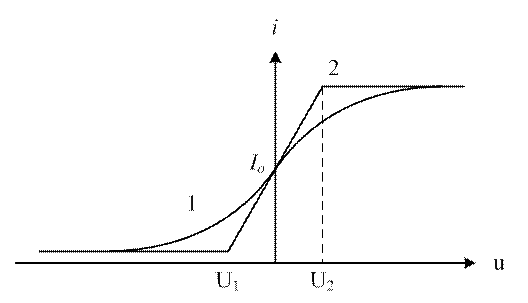
1 – плавно меняющаяся, 2 – аппроксимирующая.
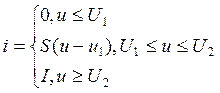
S=I/(U2-U1) – крутизна характеристики на наклонном участке;
Io – ток нелинейного элемента при U=0;
I – ток насыщения;
U1, U2 – напряжение нижней и верхней отсечки тока.
3. Спектральный анализ методом тригонометрических функций кратного аргумента.
Задача спектрального анализа заключается в определении спектра тока нелинейного элемента при воздействии на него гармонического напряжения. Этот метод основан на использовании полиномиальной аппроксимации характеристики нелинейного элемента.
Воздействие может быть гармоническим (1 синусоидальное колебание), бигармоническим (2 синусоидальных колебания), полигармоническое (несколько).
а) гармоническое.
u=Umcos(ωot+φ); i=ao+a1Umcos(ωot+φ)+a2Um2cos2(ωot+φ)+...+anUmncosn(ωot+φ); cos2ψ=1/2+(1/2)cos2ψ; cos3ψ=(3/4)cosψ+(1/4)cos3ψ; cos4ψ=3/8+(1/2)cos2ψ+(1/8)cos4ψ; cos5ψ=(5/8)cosψ+(5/16)cos3ψ+(1/16)cos5ψ; и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.