Пассивные LC фильтры представляют собой реактивный лестничный фильтр.
Zвх1(р) – операторное входное сопротивление, нагруженное Rн.
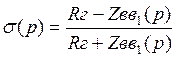 ,
, 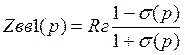
σ – коэф отражения
σ(р)σ(-р)=1-Нр(р)Нр(-р)
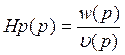
σ(р)σ(-р)=1- 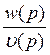
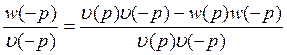
Реализация 2хполюсника с Zвх1(р) осуществляется разложением цепной дроби по методу Кауэра. Для этого порядок знаменателя должен быть > порядка числителя. Поэтому реализуется входная проводимость.
Аналогично решается задача пассивных фильтров > высокого порядка. ФНЧ 5го порядка может быть построен
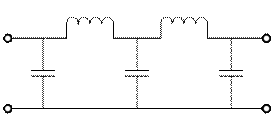
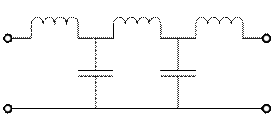
Фильтры Баттерворта отличаются от Чебышева только разными значениями параметров реактивных эл-тов, получ-х в процессе реализации соотв-х передаточных ф-ий. Реализация Rвх фильтров со всплесками ослабления приводит к схемам, содержащим резонансные контуры. Для схемы ФНЧ 5го порядка со всплесками ослабления могут выглядеть так
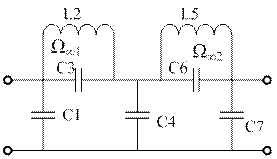
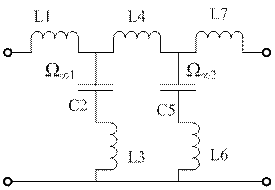
В 1й схеме в ||-х контурах возникают резонансы токов на частотах Ω∞1, Ω∞2. R контуров на этих частотах принимает бесконечно большое значение. На этих частотах происх как бы обрыв продольных ветвей и сигнал на этих частотах бесконечно велик. Во 2й схеме в последовательных контурах возникает резонанс напряжений на частотах Ω∞1, Ω∞2. R контуров на этих частотах обращается в 0, поперечные ветви закрачивают сигнал и сигнал не проходит.
34. Реализация активных RС-фильтров нижних частот.
Достоинства:
- возможность усиления сигнала в ПП
- отсутствие L (нетехнологичный эл-т)
- малые габариты и вес
- легкость настройки
- простота реализации фильтров высоких порядков путем каскадного соединения звеньев.
Недост:
- необх-ть дополнительного ист питания
- невысокие частотные св-ва (поэтому строятся на НЧ)
- температурная нестабильность
- невозможность применения в силовых цепях.
Активный RC фильтр предст собой комбинацию пасс RC и акт эл-та, в кач-ве кот исп-ся ОУ с 2мя входами. Идеальный ОУ это ИНУН с б/б Ку, б/б Rвх и б/м Rвых. Порядок реализации. Полученную по ЧХ прд-ую ф-ию Нр(Р), порядка n разбивают на произв-ые ф-ии не выше 2го порядка. Нр(Р)=Нр1(Р)Нр2(Р)Нрn(Р). Реализуют звеньями 1го и 2го порядка. Схему всего фильтра получают путем каскадного соединения всех фильтров. В практике проектирования исп-ся большое число схем, реализ-х прд-ую хар-ку 1го, 2го порядка.
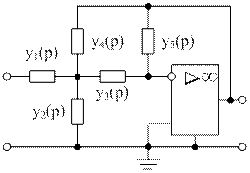
Hp(P)=U2(P)/U1(P)
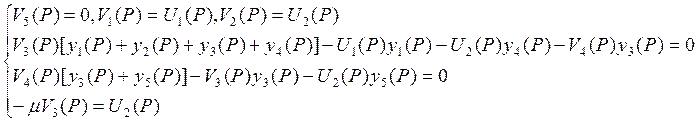
V3, V4 – исключить
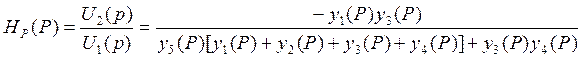
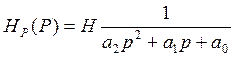
В схеме следует принять у1(р), у3(р), у4(р) активными → G1, G3, G4, у2(р), у3(р) → рС2, рС5.
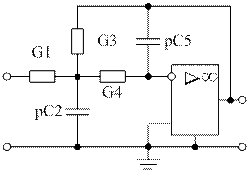
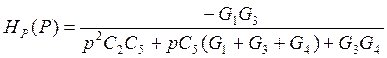
Сопоставлением коэф-в при Р в соотв-х степенях и свободных членов прд-ой ф-ии можно сост сист ур-ий из которых опред-ть парамтры эл-тов схемы, величины R и C. С2С5=а2, С5(G1+G3+G4)=а4, G3С4=а1. Т.к. в ур-ии неизв-х 5, а ур-ий 3, параметрами 2х эл-тов задаются добровольно, придавая им подходящее приемлемое значение. Параметры остальных эл-тов находятся.
35. Переход от фильтров нижних частот к фильтрам верхних частот и полосовым. Преобразование частоты.
От хар-к ФНЧ можно перейти к хар-кам фильтров других типов. Для этого во всех выражениях, содержащих переменную ω следует провести замену переменной таким образом, чтобы хар-ки ФНЧ перешли в хар-ки соотв-х фильтров. Подобная замена переменной наз-ся преобразованием частоты, а исходный ФНЧ наз-ся ПЧ-прототипом.
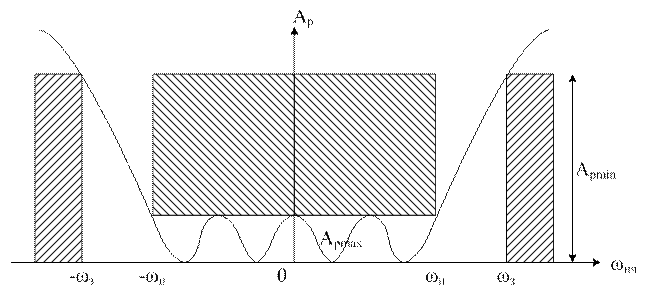

Преобразовать хар-ку ФНЧ в ФВЧ можно подставив ωнч=-ωп2/ωвч. ωп – граничная частота ПП. ωвч=-ωп2/ωнч. ωнч=-∞, ωвч=0
ωнч=-ωп, ωвч=ωп
ωнч=0, ωвч=-∞
ФНЧ→ПФ
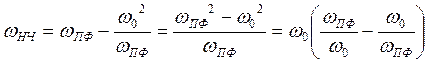
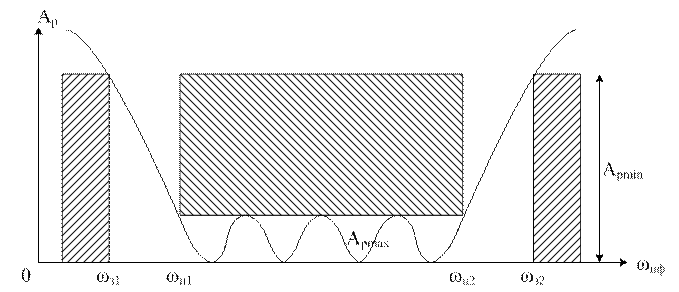
ωнч=-∞, ωпф=0
ωнч=0, ωпф=ωо
ωнч=∞, ωпф=∞
![]() - (центр) средняя
геом частота ПФ.
- (центр) средняя
геом частота ПФ.
36. Преобразование схем пассивных LС-фильтров при переходе от фильтров нижних частот к фильтрам верхних частот и полосовым.
ФНЧ→ФВЧ
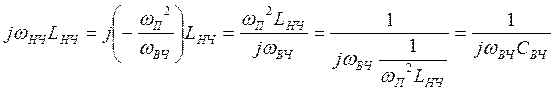
Индуктивное R переходит в
емкостное 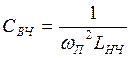
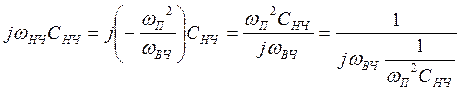
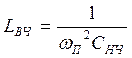
ФНЧ→ПФ
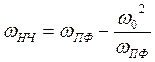
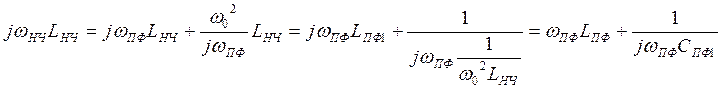
LПФ=LНЧ, 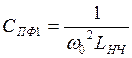
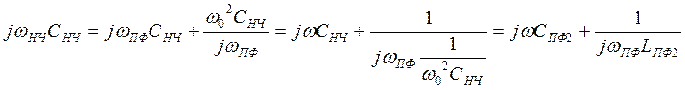
СПФ=СНЧ, 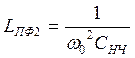
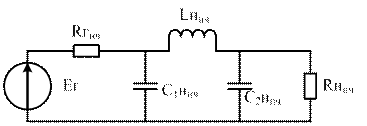
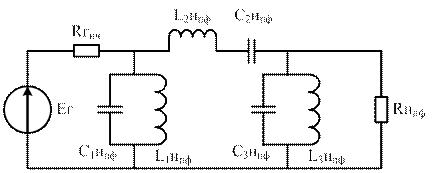
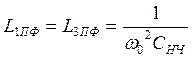
С1пф=С3пф=С1нч=С3нч
L2ПФ=L2НЧ, 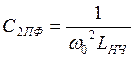
ωо – центр частота ПФ
37. Преобразование передаточных функций активных RC-фильтров при переходе от фильтров нижних частот к фильтрам верхних частот и полосовым и их реализация.
ФНЧ→ФВЧ
Для перех от прд-ой ф-ии ФНЧ к ФВЧ необх осущ замену компл-ой перем-ой f.
ωнч=-ωп2/ωвч, jωнч=ωп2/jωвч, jΩнч=1/jΩвч, Ωнч=-ωнч/ωп, Ωвч=-ωвч/ωп, fнч=1/fвч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.