14. Устойчивость. Критерии устойчивости. Условие самовозбуждения автогенератора.
Для определения условий самовозбуждения автогенератора используют линейную теорию, т.к. первоначально возникающие колебания имеют малую амплитуду, затрагивая небольшие участки характеристик, которые можно считать линейными, а параметры постоянными. Возникновение колебаний можно рассматривать как потерю системой устойчивости и процесс самовозбуждения автогенератора рассматривать на основе общей теории устойчивости. В состоянии устойчивости система может быть только стационарной, т.е. система находится в состоянии покоя или периодического колебательного движения. Устойчивой считается та система, в которой будучи выведенной из стационарного состояния кратковременным внешним воздействием (возмущением) оно возвращается в прежнее стационарное состояние. Отсюда вытекает уравнение устойчивости. В уравнение стационарного состояния вводится возмущение и исследуется решение нового уравнения. Если это решение стремится к решению, соответствующему стационарному состоянию, то система устойчива. В противном случае неустойчива. Пусть стационарное состояние описывается уравнением
Х0(t) – ток или напряжение, соответствующее стационарному состоянию
f(t) – воздействие постоянной или периодической функцией времени
am÷a0 - постоянные
Х – возбуждение
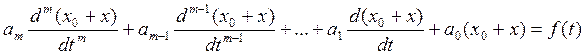
Это уравнение можно разбить на два
- 1ое уравнение
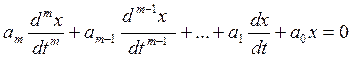- 2ое уравнение
1 – уравнение системы в стационарном режиме (до возмущения)
2 – система в свободном режиме
Решение этого уравнения однозначно отвечает на вопрос об устойчивости. Если x(t) будет иметь характер затухания, то колебательная система устойчива.
По 2 уравнению составляем характеристическое уравнение.
(3)
рi –корни ур-я
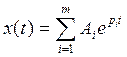
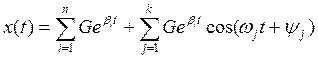
Для того чтобы сист была устойчивой, все слагаемые должны затухать, слагаемые экспоненты должны быть отриц-ми. Если хотя бы 1 из вещ-х корней или пара компл-х слаг-х будет больше 0 сист потеряет устойчивость. Корни характеристич-го ур-я зав-т от коэф am÷ao и при опред-ой комбинации этих коэф веществ-ой части эти корни получаются отрицательными. Можно устан-ть усл-е которое гарантирует получение уст-х сост-й. Эти усл-я получили название критерия устойчивости. Критерии устойчивости опред усл-е при кот все корни имеют отриц вещ части. Наиболее употребит-ми явл-ся критерии Рауса-Гурвица или Найквиста-Михайлова. Для того чтобы вещ части всех корней хар-го ур-я (3) больше 0, необх и дост-но чтобы были положительны все опред-ли Гурвица.
15. Стационарный режим работы автогенератора. Средняя крутизна. Баланс амплитуд. Баланс фаз.
В процессе нарастания колебаний усиление k-цепи непрерывно изменяется. С ростом амплитуды колебаний усиление k-цепи ↓. Если амплитуда не ↑, это значит, что в автогенераторе установился стационарный режим. Выходное напряжение имеет постоянную амплитуду и форму близкую к синусоидальной. Соотношение между мгновенным значением можно считать линейной. Линейность нарушается при переходе на другую амплитуду и другому стационарному режиму. В стационарном режиме форма тока и напряжения синусоидальны, поэтому можно применить символический метод анализа. Расчет ведется по первым гармоникам тока и напряжения. Генератор состоит из 2х частей: нелинейной (VT) и линейной (контур, катушка связи).
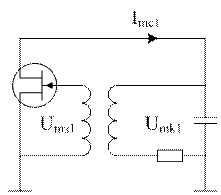
Umk1 – амплитуда 1й гармоники напряж на контуре
Umk1=Imc1·Iэ (1)
Umз1=Коc·Umk1 (2)
Подставим (2) в (1)
Umз1=Коc·Zэ·Imc1 (3)
Под средней крутизной будем понимать
Sср=Imc1/Umз1
Imc1=Sср·Umз1 (4)
Umз1=Sср·Коc·Zэ·Umз1
Sср·Коc·Zэ=1
В стационарном режиме компл коэф прд по замкнутому кольцу автогенератора = 1.
Sср=Sср·еjφs
Коc=Коc·еjφk
Zэ=Zэ·еjφz
Sср·Коc·Zэ·еj(φs+φk+φz)=1
φs+φk+φz=0;2π;4π,…,nπ (n=0,1,2,…) (5)
Sср·Коc·Zэ=1 (6)
(5) – уравнение БФ. Оно означает, что в стационарном режиме сумма всех фазовых сдвигов по замкнутому кольцу автогенератора = 0 или целому числу 2П. Каждый из сдвигов зависит от частоты по-разному. Существует лишь одна частота, на которой выполняется условие БФ, и на которой возможна генерация колебаний.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.