52. Уравнения передачи длинной линии в гиперболических функциях. Входное сопротивление.
U и I в конце лини
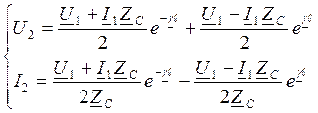
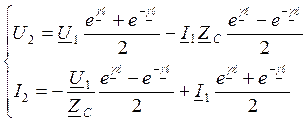
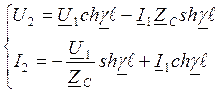
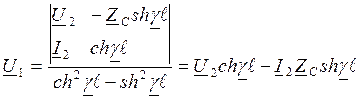
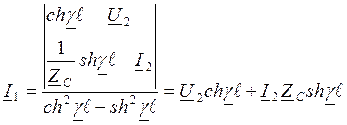
U1=U2chγℓ+I2Zcshγℓ
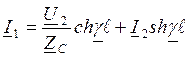
shγℓ=Sejφschγℓ=Cejφc
sh(x+jy)=Sejφs
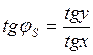
ch(x+jy)=Cejφc
x=αℓ, y=βℓ, γ=α+jβ
sh(αℓ+jβℓ)=shαℓcosβℓ+jchαℓsinβℓ
ch(αℓ+jβℓ)=chαℓcosβℓ+jshαℓsinβℓ
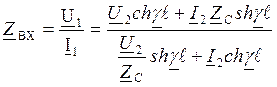
U2=I2ZH
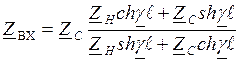
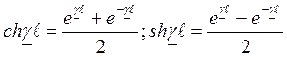
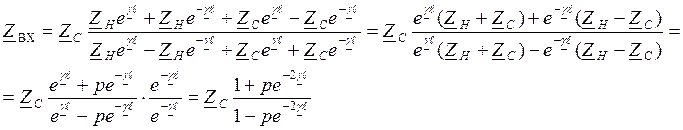
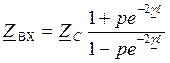
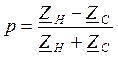- коэф
отражения
53. длинная линия в режиме согласованной нагрузки.
ZH=ZC – согл режим
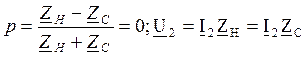
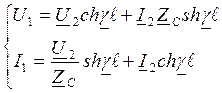
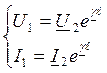
Амплитуда падающей волны изменяется по ехр з-ну
Собств-ое ослабление линии А=αℓ хар-ет отличие мощности в конце и начале линии.
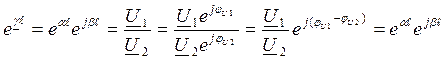
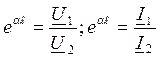
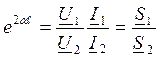
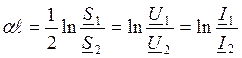
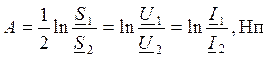
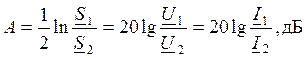
β=βℓ=φu1-φu2=φi1-φi2 – коэф фазы
54. Искажения в линиях связи. Линия без искажений.
При прд син-х колеб-й амплитуды и фазы мгновенных значений напряжения и тока в режиме согласованной нагрузки будет меняться вдоль лини, но форма меняться не будет. Условие сохранения соотношения м/у амплитудой и фазой – постоянство АЧХ и ФЧХ. Если по линии распространяется периодич-й и непериодич-й сигнал, то составляющие спектра сигнала будут претерпевать различные изменения и форма сигнала в нагрузке изменится.
Причины иск-й:
а) зав-ть собств-го ослабл-я от частоты б) нелинейное изменение собственной фазовой постоянной в) отражение в начале и конце линии из-за неравенств сопротивлений
Пусть линия согл и отр в нач и конце линии отсутствует. Если коэф ослабления зав-т от частоты, составляющая спектра сигналов поступает в нагрузку с различными собственными ослаблениями и форма сигнала искаж-ся. Такие искаж-я наз-ся амплитудно-частотными. Условием согласования явл-ся постоянство АЧХ во всем спектре частот.
Если Lo зависит от частоты, то составляющие спектра будут распр-ся с различной скоростью. Эти искаж-я наз-ся фазо-частотными. Усл-ем устран-я этих искаж-й β должна быть линейной функцией частоты. Для устранения отраж-й ZH=ZГ=ZC
55. Режим бегущих волн в линии без потерь.
При исслед-ии фидерных линий в радиосвязи и в коротких отрезков коакс-х кааб-х линий можно положить α≈0 и коэф распр γ=jβ. В такой линии амплитуды падающих и отраж-х волн не затухают. Линия удовлетворяет этому усл-ю наз-ся линией без потерь (Ro≈0; Go≈0).
α=0,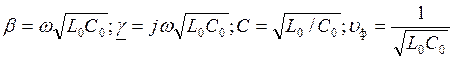
Если эти усл-я сравнить с условиями прд можно сделать вывод, что линия без потерь не вносит амплитудно-частотных и фазо-частотных искаж-й.
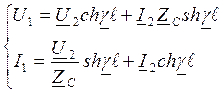
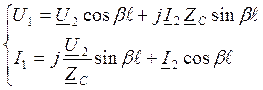- ур-я прд для
линии без потерь
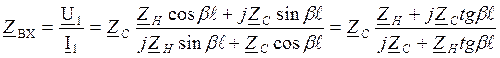
В зав-ти от нагрузки может быть 3 режима: стоячих, бегущих, смеш-х волн.
Режим БВ будет, если ZH=ZC, р=0
В линии будут существовать только падающие (БВ), U и I в любой точке х:
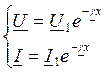- ур-я для согл
линии
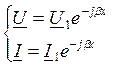
U и I будут менятся:
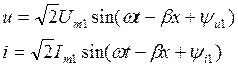
Амплитуды напряж-й и тока вдоль линии не меняется.
56. Режим стоячих волн в линии без потерь. Входное сопротивление.
Будет при ХХ иКЗ
1) ХХ. ZH=∞
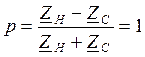
I2=0. y – расстояние от конца линии
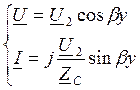
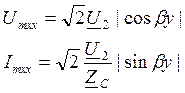
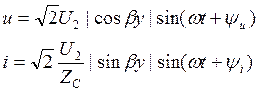
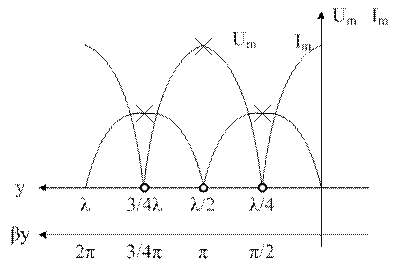
х – пучности Um, Im
о – нули Um, Im
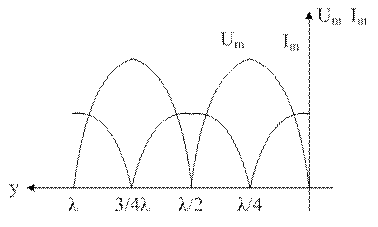
Такое представление тока и напряги в этом режиме за счет интерф падающ и отраж волн, кот распростр-ся без потерь и имеют равные амплитуды. Когда их фазы один – пучность, фазы разные – нули.
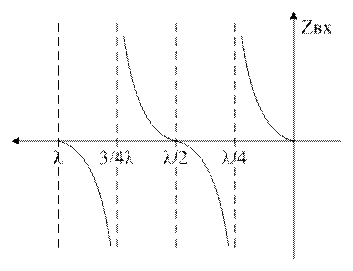
Хар-р зависимости от длины отрезка линии
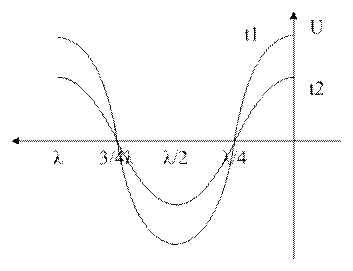
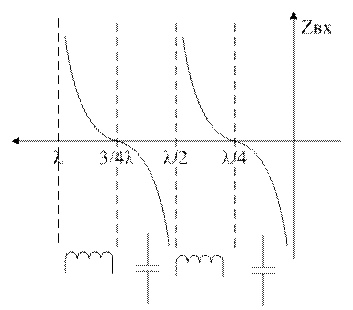
Zвх в ДЛ в ХХ реакт-но.
- емк хар-р
- инд хар-р
2) КЗ
ZH=0, р=-1, U2=0 (напряга в конце линии)
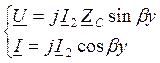
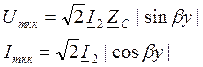
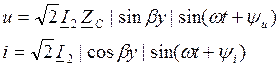
57. Режим смешанных волн в линии без потерь.
ZH=RH≠ZC
В них будет БВ и СВ
Картина распред-я амплитуд вдоль линии будет зав-ть от соотнош-я RH и ZC. Степень пульсации напряж-я вдоль линии оценив-ся коэф-м БВ.
КБВ=Umin/Umax
КСВ=1/КБВ
m=ZC/RH
1) ZC<RH; m<1; КБВ=m
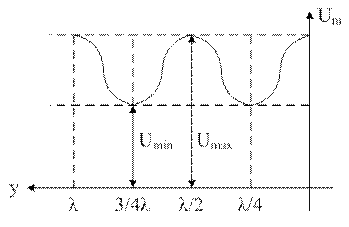
2) ZC>RH; m>1; КБВ=1/m
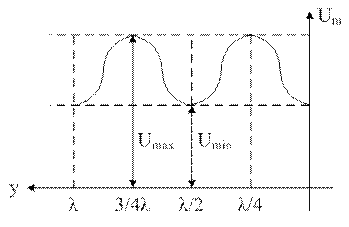
р – коэф отраж-я. p=U0/Um
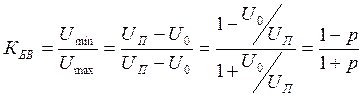
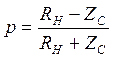- коэф отраж-я в
конце линии
58. Практическое использование отрезков длинных линий без потерь.
1) Соглас-е нагрузки с ДЛ при помощи четвертьволнового отрезка.
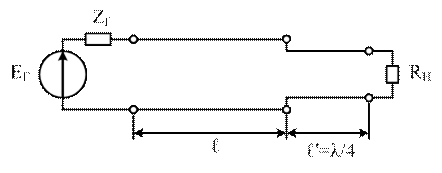
Если ZC≠RH в ней возникает искаж-я. Для устранения этих искаж-й м/у линией и нагрузкой включают ¼ волновый отрезок. ℓ'=λ/4, тогда βℓ`=π/2
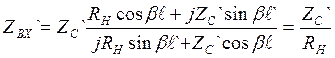
ZВХ`=ZC
Подбираем параметры: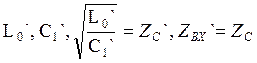 
В линии будет режим БВ, а в ¼ волновом отрезке будут смешанные волны.
2) Использование ¼ волнового отрезка в кач-ве КК.
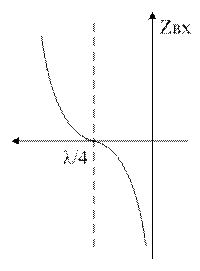
¼ волновый отрезок разомкнутый на конце имеет ZВХ
¼ волновый отрезок разомкнутый на конце эквивалентен настроенному в резонанс послед-й КК. При ↓ частоты ZВХ приобретает емкостной хар-р, при ↑ частоты – индукт-й хар-р.
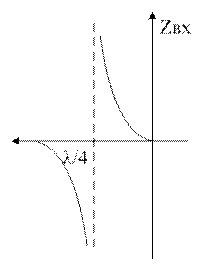
3) ¼ волновый отрезок замкнут на конце
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.