fд задается генератором имп синхр-ии. В момент подачи сигнала синхр-ии на АЦП на его выходе возникает сигнал отображающий сигнал x(t) в данный момент времени в виде двоичного числа с опред-м кол-вом разрядов. Этот сигнал поступает в арифм устр-во цифр процессора, где над цифрами произв-ся нужные операции: сложение, вычитание, деление, сдвиг во времени на заданное число интервалов дискр-ии. В устр-ве памяти могут сохр-ся рез-ты. Цифр проц-р преобр-ет поступающие на него числа соотв-но алгоритмам цифровой фильтрации и создает на выходе посл-ть двоичных сигналов, которые при необх-ти преобр-ся в ЦАП в анал сигн. Быстродействие обесп-ся примен-ем БИС.
44. Теорема свертывания для дискретных сигналов.
Линейная сист преобразует вх-й сигнал x(t) в дискр-й y(t)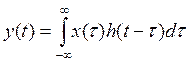 
, h(t) – имп хар-ка
Для линейного ЦФ смещение входного сигнала на любое число шагов дискретизации вызывает такое же смещение имп-ой хар-ки.
Если на входе ЦФ с имп хар-кой (h0, h1, h2,…) действует некоторый сигнал (х0, х1, х2), то на выходе появл-ся сигнал (у0, у1, у2,…, уm,…, уn). уm=х0hm+х1hm-1+х2hm-2+…+хmh0
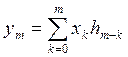
Это и есть дискретная свертка вх-го сигнала и дискр имп хар-ки цепи и выходная посл-ть есть посл-ть сигналов, каждый из которых есть свертка вх-го сигнала и дискр-ой имп хар-ки.
45. Z-преобразование для дискретных сигналов и его свойства. Обратное 2- преобразование
При анализе и синтезе дискр-х и цифр-х устр-в
широко исп-ся так называемое Z-преобраз-е, которое явл-ся
формальной аналогией преобраз-я Лапласа и Фурье для непрер-х сигналов. Суть Z-преобраз-я для дискр-го сигн закл-ся в том, что числовая посл-ть {xk}=(x0x1x2…) замен-ся суммой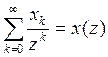 
Замена послед-ти 1 и 0 алг-м выр-ем позволяет изучать св-ва методами матанализа.
Св-ва z-преобраз-я:
а) линейность. Если {xk} и {yk} некоторые дискр числа, имеющие некоторые дискр-ые преобраз-я X(z) и y(z).
{Uk}={αxk+βyk}, U(z)=αX(z)+βy(z)
б) z-преобраз-е смещенного сигнала. Если дискр сигнал{xk} перен-ся на 1 позицию в сторону запаздывания, то это сдвигу будет соотв-ть умножение его z-преобраз-я на z-1
yk=xk-1
y(z)=x(z)·z-1
в) z-преобраз-е свертки дискр-х сигналов. Если на вход с имп-ой хар-кой д-ет дискр сигнал {xk}=(x0x1x2…) на выходе будет иметь дискр сигнал.
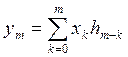
уm=х0hm+х1hm-1+х2hm-2+…+хmh0
г) обратное z-преобраз-е. Если сущ-ет z-преобраз-е {xk}÷X(z), то m-й отсчет сигн опред-ся как
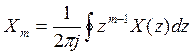
46. Системная функция цифрового фильтра и частотный коэффициент передачи.
Част-й коэф прд анал сигн можно опред-ть с пом-ю преобраз-я Фурье от имп хар-ки цепи
Если сигнал дискр-й, то имп хар-ка есть посл-ть дискр-х отсчетов {hk}=(h0h1h2…) и част-й К прд К(jω)=ΣhkejωΔk (1)
Δ – шаг дискретизации
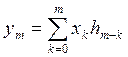
y(z)=x(z)H(z)
(2) – системная
ф-ия ЦФ.
Из сравнения (1) и (2) можно увидеть, что для получения К(jω) достаточно выр-е для Z-преобраз-я дискретной имп хар-ки цепи {hk}=Н(z) z=ejωΔ
H(z)=y(z)/X(z)
Для получения компл коэф прд дискретной цепи нужно выр-е подставить z=ejωΔ
47. Реализация алгоритмов цифровой фильтрации. Нерекурсивный и рекурсивный фильтры.
В идеальном ЦФ для формир-я цифрового сигнала в i-й момент времени исп-ся:
а) знач-е вх-го сигнала в момент i-го отсчета и некоторое число предшеств-х вх-х отсчетов б) некоторое число предшеств-х вых-х сигналов
В зав-ти от того как исп-ся инф-я о прошлом состоянии системы сущ-ют ЦФ различных классов. В рекурсивных исп-ся предшествующие отсчеты вх-го сигн. Вых-й сигнал форм-ся в соотв-ии с алг уi=a0xi+a1xi -1+a2xi -2+…+anxi-n
a0, a1, an – послед-ть коэф
n – порядок фильтра
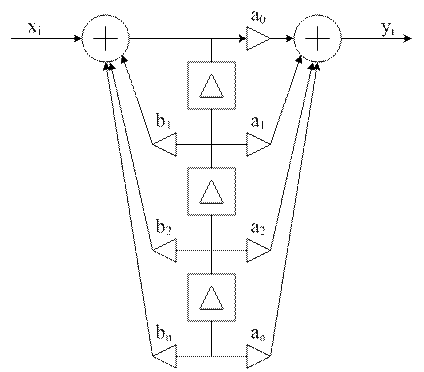
Системная ф-ия имеет n-кратный полюс и n-корней, корд которых опред-ся коэф-ми фильтра. Алг р-ты рекурс-го фильтра можно пояснить с пом-ю сх
z-1 – блок задержки на 1 шаг дискретиз-ии
Алгоритм дискр-ой обраб сигнала закл-ся в том, что сначало реализ-ся рекурсивное преобраз-е, а затем нерекурсивное, и стр сх получ-ся такой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.