Наличие ОС может придать неуст-ть когда большое по амплитуде возд-е вызывает бесконечно нарастаемый отклик. Известно, что у устойчивой анал цепи полюсы прд-ой ф-ии распол-ся в левой полупл-ти компл-ой перем-ой Р. При перех от анал цепи к дискр и замене преобраз-я Лапласа z-преобраз-е точки левой полупл-ти переходят к точке, лежащей внутри еденичной окр-ти z-пл-ти. Аналоговая цепь устойчива если полюсы прд-ой ф-ии нах-ся в левой полупл-ти. При замене преобраз-я Лапласа z-преобраз-ем перех-т к точке, лежащей внутри окр-ти. После прд-ой ф-ии устойчивой дискр-ой цепи распол-ся внутри единичной окр-ти z-пл-ти. Нерек фильтры всегда устойчивы.
48. Амплитудно-частотные искажения в электрических цепях. Корректоры амплитудно-частотных искажений.
Одним из усл-й при проектир-и канала связи явл-ся требов-е отсутствий часто-х иск-й (ЧИ). Под ЧИ поним-ся такие искаж-я, которые обусловлены частотной зависимостью параметров канала связи. Канал можно рассм-ть как 4хполюсник и его св-ва опис-ся компл-ой мерой прд γ Г=A+jB. Усл-ие отсутствия в канале искаж-й, чтобы во всем спектре передаваемых частотных сост-х нужно A(ω)=const=A, B(ω)=τω+kπ; τ, k – const. Записанные условия определяют, что пост ослабления не зависило от частоты, а пост-ая фазы была пропорциональна частоте. В этом случае U в канале связи будет подобно U, прилож-му в канале связи. Борьбу с ЧИ осущ-ся с пом-ю корр-в.
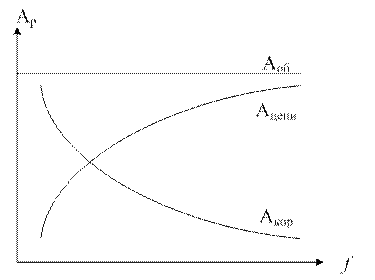
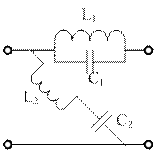
В числе амплит-х корр-в примен-ся Т-обр и Г-обр сх 4хпол-ков.
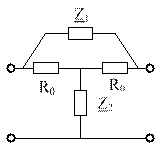
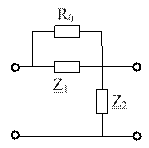
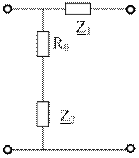
Z1 и Z2 делаются взаимно обратимые. Z1Z2=R02, тогда
входные сопрот-я 4хпол-ков не зависят от частоты. Rн=R0. 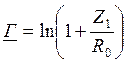 .
В кач-ве Z1 стоит ||-й
участок R1 и X1, а в кач-ве Z2 R2X2
.
В кач-ве Z1 стоит ||-й
участок R1 и X1, а в кач-ве Z2 R2X2
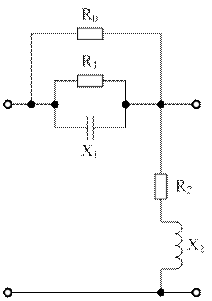
Гр-к завис-ти ослабл-я от частоты
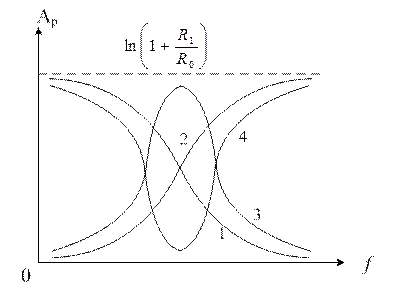
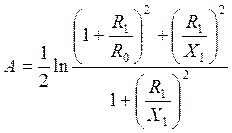
Треб-й диап-н частот ослабл-й можно изменить измен-ем X1 X2.
49. Фазо-частотные искажения в электрических цепях. Корректоры фазо-частотных искажений.
ФЧИ вызыв-ся тем, что составляющие спектра сигнала приходят в канал связи в разное время с начальными фазами, отличными от нач-х фаз. Для устр-я этих иск-й необх, чтобы фазовая пост-ая должна линейно зависеть от частоты. В кач-ве фазового кор-ра исп-ся кор-р мостового типа
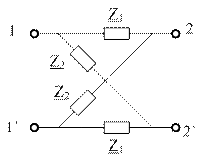
Z1 и Z2 взаимно обратимые.
Z1Z2=Ro=-X1X2
![]()
Фазовая пост-ая 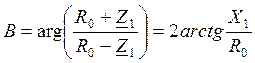
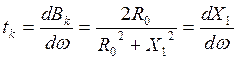

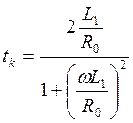
Звено наз-ся звеном 1го порядка, в каждом плече по 1му эл-ту
Хар-р зав-ти Вк от частоты опред-ся сложностью звена.
50. Длинная линия. Первичные параметры. Дифференциальные уравнения однородной линии.
Линии связи исп-ся для орг-ии проводного вещания. В радиотехнике исп-ся для прд эн-ии от ист к нагрузке. Эл св-во линии опред-ся сопротивлением и индуктивностью проводов, емкостью и проводимостью м/у проводами, равномерно распред-ми по длине линии и значения, отнесенные к единице длины линии наз-ся первичными параметрами. Если первичные параметры по всей длине линии остается пост-ми линия наз-ся однородной. Первичные параметры опред-ся материалом, частотой тока и диэл-ми св-вами окр среды. С ↑ f Ro↑, Go↑, Lo↓ из-за поверхн-го эфф-та, Со остается пост-ой.
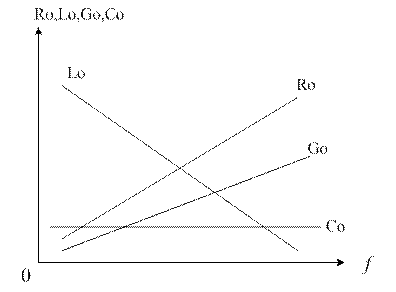
В линии ЭМ колеб-я распр-ся с конечной скоростью не превышающей скорость света, поэтому ток и напряж-е в любой точке линии явл-ся не только ф-ей времени, но и расстояния. Это основное отличие цепей с сосредоточ-ми парам от рассосредоточ-х. ДЛ считаются линии, физическая длина которых соизмерима с длинной волны. ДЛ можно предст-ть экв эл-ой цепью, состоящей из бесконечно большого числа звеньев Δх.
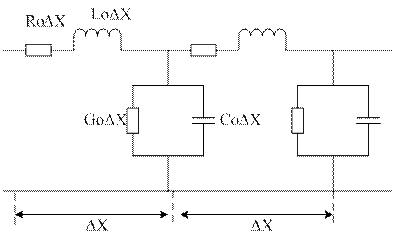
Δх – длина цепочки х – расстояние от начала линии
Ro, Go, Lo, Со – парам на ед длины Δх.
В соотв-ии с з-ми Кирхгофа
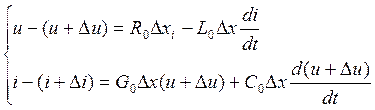
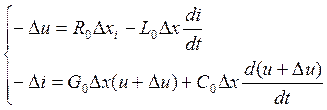
 - пренебрегаем
- пренебрегаем
Δх→0
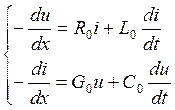 - ур-ие линии в
част-х произв-х
- ур-ие линии в
част-х произв-х
Такие ур-я получили название телеграфных ур-й.
51. Однородная линия в режиме гармонических колебаний. Вторичные параметры. Фазовая скорость. Коэффициент отражения.
По мере ↑ расстояния Х un↓ Uo↑. При неизменном значении Х un и in измен-ся по син-му з-ну. При неизм-м t=t1 un и in измен-ся по затух син
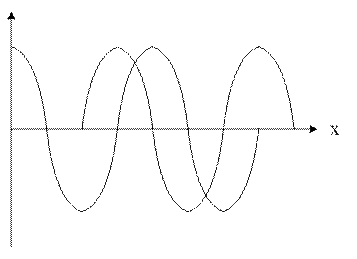
βх – собств-ая фазовая пост-ая и опред-ет фазу кол-й мгнов-х знач-й прямых и отраж-х волн.
υф – скорость распространения точки, фаза которой постоянна.
ωt-βx+φn1=const
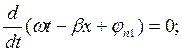
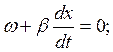
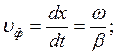
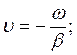
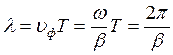
Отражение в конце линии хар-ся коэф отраж-я
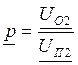
U2=I2ZH, U2=U2П+U2О
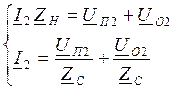

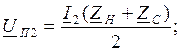
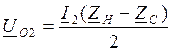
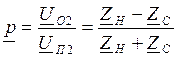
ZH=ZC, p=0
ZH=0, p=-1 - кз
ZH=∞, p=1 - хх
-1≤р≤1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.