Преобразование сигналов в нелинейных электрических цепях. Спектральная диаграмма воздействия на нелинейный элемент, страница 2

i=(a_o+(1/2)a₂U_m²+(3/8)a_nU_mⁿ+...)+(a₁U_m+(3/4)a₃U_m³+(5/8)a₅U_m⁵+...)cos(ω_ot+φ)²+((1/2)a₂U_m²+(1/4)a_nU_mⁿ+...)cos2(ω_ot+φ)+((1/4)a₃U_m³+(5/16)a₅U_m⁵+...)cos3(ω_ot+φ);

I_o=u_o+(1/2)a₂U_m²+(3/8)a_nU_mⁿ+...

I_m1=a₁U_m+(3/4)a₃U_m³+(5/8)a₅U_m⁵+...

I_m2=(1/2)a₂U_m²+(1/4)a_nU_mⁿ+...

I_m3=(1/4)a₃U_m³+(5/16)a₅U_m⁵+...

i=I_o+ I_m1cos(ω_ot+φ)+I_m2cos2(ω_ot+φ)+I_m3cos3(ω_ot+φ)+...

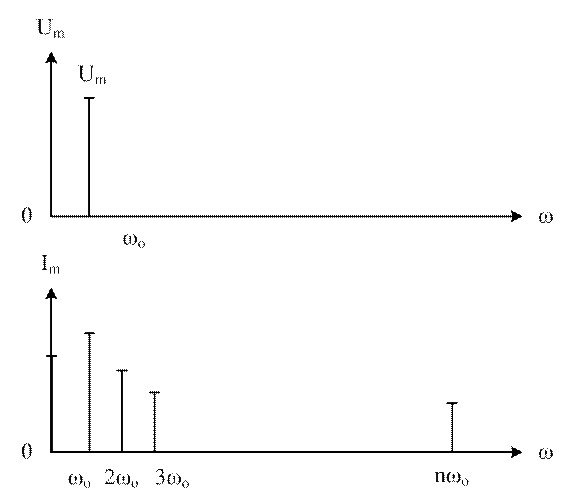
Выводы:

- спектр тока линейчатый, содержит гармоники = частоте воздействующего колебания; № высшей гармоники = степени полинома.

- постоянная составляющая и амплитуды четных гармоник тока определяется четными степенями напряжения в полиноме, а нечетные нечетными.

- текущая фаза ψ_k k-ой гармоники тока с частотой ω_к=kω_o в k-раз больше текущей фазы воздействующего напряжения ψ_к=k(ω_ot+φ)=kω_ot+kφ=ω_кt+φk.

б) бигармоническое.

u=u₁+u₂=U_m1cos(ω₁t+φ₁)+U_m2cos(ω₂t+φ₂)

i=a_o+a₁u+a₂u²

i=a_o+a₁U_m1cos(ω₁t+φ₁)+a₁U_m2cos(ω₂t+φ₂)+a₂U_m1²cos²(ω₁t+φ₁)+ a₂U_m2²cos²(ω₂t+φ₂)+2a₁U_m1U_m2cos(ω₁t+φ₁)cos(ω₂t+φ₂).

cos²ψ=1/2+(1/2)cos2ψ

cosψ₁cosψ₂=(1/2)(cos(ψ₁-ψ₂)+cos(ψ₁+ψ₂))

ψ₁=ω₁t+φ₁; ψ₂=ω₂t+φ₂;

i=a_o+(1/2)a₂U_m1²+(1/2)a₂U_m2²+a₁U_m1cos(ω₁t+φ₁)+a₁U_m2cos(ω₂t+φ₂)+(1/2)a₂U_m1²cos2(ω₁t+φ₁)+(1/2)a₂U_m2²cos(ω₂t+φ₂)+a₂U_m1U_m2cos((ω₁-ω₂)t+(φ₁-φ₂))+a₂U_m1U_m2cos((ω₁+ω₂)t+(φ₁-φ₂));

I_o=a_o+(1/2)a₂U_m1²+(1/2)a₂U_m2²

I_m10=a₁U_m1 - амплитуда 1й гармоники 1й частоты

I_m01=a₁U_m2 - амплитуда 2й гармоники 1й частоты

I_m20=(1/2)a₂U_m1² – амплитуда 1й гармоники 2й частоты

I_m20=(1/2)a₂U_m2² - амплитуда 2й гармоники 2й частоты

I_m11=a₂U_m1U_m2 – амплитуды комбинационных гармоник

i=I_o+ I_m10=cos(ω₁t+φ₁)+I_m01cos(ω₂t+φ₂)+I_m20cos2(ω₁t+φ₁)+I_m02cos2(ω₂t+φ₂)+I_m11cos((ω₁-ω₂)t+(φ₁-φ₂))+I_m11cos((ω₁+ω₂)t+(φ₁+φ₂))

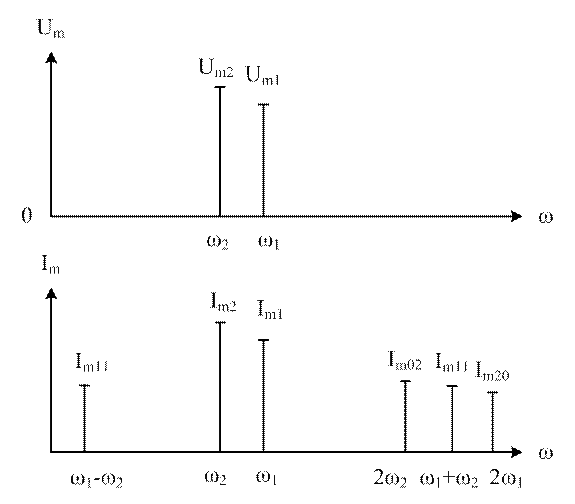
Выводы:

-по сравнению с гармоническим воздействием появились составляющие с комбинационными частотами ω₁-ω₂, ω₁+ω₂;

-в спектре присутствуют гармоники u₁ω₁ частоты ω с начальными фазами k=1,2,...n;

-в спектре присутствуют гармоники u₂ω₂ частоты ω с начальными фазами k=1,2,...n;

4. Спектральный анализ методом угла отсечки.

Метод применяется при больших амплитудах воздействующего гармонического напряжения. Используется кусочно-линейная аппроксимация ВАХ НЭ.

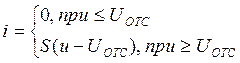
Ток через НЭ протекает в течение части периода. Половина этой части в градусах или радианах называется углом отсечки Θ. Если ωt=Θ, то напряжение достигает значение u(t)=U_o+U_mcosωt=U_o+cosΘ=U_отс. cosΘ=(U_отс-U_o)/U_m.

i≠0, i=S(u-U_отс), i=SU_o-SU_mcosωt-SU_отс. Если ωt становится равным Θ, то i=0. 0=SU_o+SU_mcosΘ-SU_отс. i=SU_m1(cosωt-cosΘ).

Ток представляет собой периодическую последовательность ряда Фурье. Он может быть записан в виде i=I_o+I_m1cosωt+I_m2cos2ωt+I_m3cos3ωt+...

Коэффициенты определяются по формулам

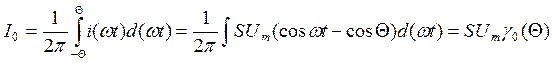
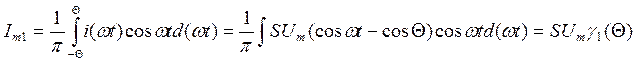
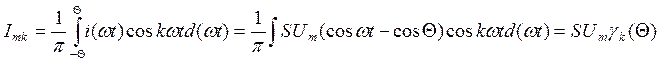
γ_o, γ₁, γ_k – коэффициенты Берга

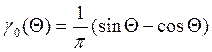
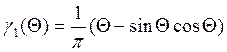
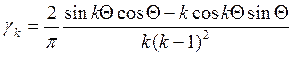
Коэффициенты зависят от угла отсечки. Они приводятся в справочниках.

Максимальные значения коэффициентов и амплитуд соответствующих гармоник принимают при Θ=180/k, k – номер гармоники.

I_mk=SU_mγ_k(Θ), k=0,1,2...

ωt=0, i=i_max, i_max=SU_m(1-cosΘ), , .

, , ,

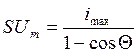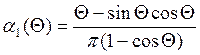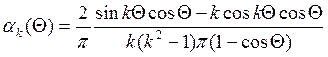
5. Метод пяти и трех ординат.

Метод не требует предварительной аппроксимации характеристики НЭ и называется графоаналитическим.

а) 5 ординат.

Позволяет определить постоянную составляющую и амплитуды 1х 4х гармоник тока.

i=I_o+I_m1cosωt+I_m2cos2ωt+I_m3cos3ωt+I_m4cos4ωt (1)

I_o÷I_m4 – определяются из условия, что в 5 выбранных точках ординаты приближенного выражения совпадают с ординатами ВАХ. В качестве таких точек берут такие значения u,i,t в которых ωt=0, π/3, π/2, 2π/3, π.

Подставим в (1) ωt=0: i_max=I_o+I_m1+I_m2+I_m3+I_m4; ωt=π/3: i₁=I_o+0,5I_m1-0,5I_m2-I_m3-0,5I_m4; ωt=π/2: i_о=I_o-I_m2+I_m4; ωt=2π/3: i₂=I_o+0,5I_m1-0,5I_m2+I_m3-0,5I_m4; ωt=π: i_мин=I_o-I_m1+I_m2-I_m3+I_m4. I_o÷I_m4 – неизвестные.

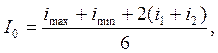
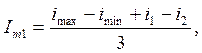
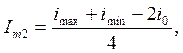
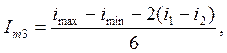
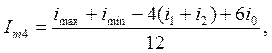
Для проверки правильности вычисления I_m0÷I_m4 рекомендуется после их нахождения подставить в (1) или сложить их и результат должен быть = i_max.

2) 3х ординат.

Позволяет определить постоянную составляющую и амплитуды 1х 2х гармоник. Он основан на совпадении тока с действительными значениями в 3х выбранных точках рабочего интервала ВАХ: i_max, i₀, i_min.

ωt=0, π/2, π.