Пусть U1 и U2 неизвестные.
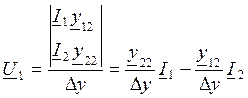
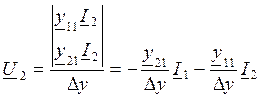
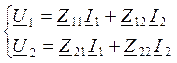
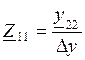 ,
, 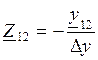 ,
, 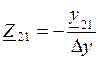 ,
, 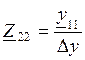
22. Определение параметров четырехполюсников.
Существует несколько способов определения параметров. Один из них заключается в приравнивании коэф-в соответствующих уравнений 4хполюсников. Метод применим для простых схем. Сложная схема может быть разбита на простые, а затем рассматривать соединения схем и находить параметры сложной схемы. Наиболее удобным считается метод ХХ и КЗ. Формулы для определения параметров этим методом вытекают непосредственно из уравнения передачи 4хполюсников.
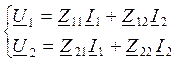
Разомкнем 2 и 2`, т.е. режим ХХ на выходе и I2=0
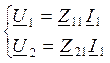 , Z11=U1/I1, Z21=U2/I1
, Z11=U1/I1, Z21=U2/I1
Разомкнем 1 и 1`, т.е. режим ХХ на выходе и I1=0
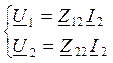 , Z12=U1/I2,
Z22=U2/I2
, Z12=U1/I2,
Z22=U2/I2
Z11, Z12, Z21, Z22 – параметры ХХ
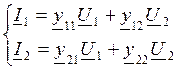
Замкнем 2 и 2`, т.е. КЗ на выходе U2=0
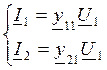 , y21=I1/U1,
y21=I2/U2
, y21=I1/U1,
y21=I2/U2
Замкнем 1 и 1`, т.е. КЗ на входе U2=0
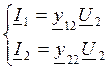 , y12=I1/U2, y22=I2/U2
, y12=I1/U2, y22=I2/U2
у11, у12, у21, у22 – параметры КЗ
При определении параметров сложного 4хполюсника можно рассматривать а) каскадное включение

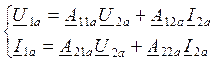 - для 1го
4хполюсника
- для 1го
4хполюсника
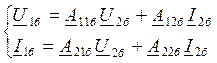 - для 2го
4хполюсника
- для 2го
4хполюсника
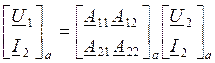 ,
, 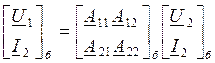 ,
,  ,
, 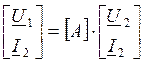
б) последовательное соединение
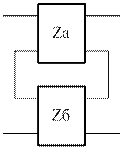
U1=U1a+U1б, U2=U2a+U2б
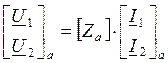 ,
, 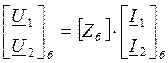
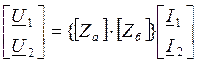 ,
, 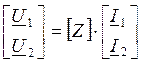
в) || соединение
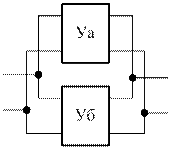
U1=U1a=U1б, U2=U2a=U2б
I1=I1a+I1б, I2=I2a+I2б
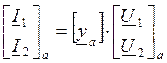 ,
, 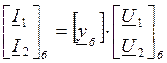
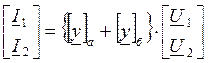 ,
, 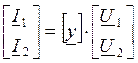
[y]=[y]a+[у]б – квадратная матрица у-параметров результирующего 4хполюсника равна сумме квадратных матриц у-параметров совмещенных 4хполюсников.
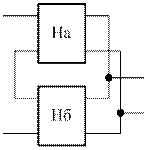
г) последовательно-|| соединение
[Н]=[Н]a+[Н]б – квадратная матрица Н-параметров результирующего 4хполюсника равна сумме квадратных матриц Н-параметров совмещенных 4хполюсников.
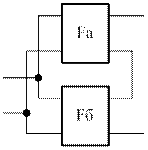
д) ||-последовательное соединение
[F]=[F]a+[F]б – квадратная матрица F-параметров результирующего 4хполюсника равна сумме квадратных матриц F-параметров совмещенных 4хполюсников.
23. Входные и характеристические сопротивления четырехполюсников.
Zвх1=U1/I1
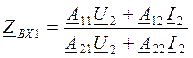 U2=I2ZH
U2=I2ZH
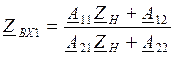
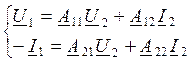
U2, I2 – неизвестные
Получим уравнение для обратной передачи энергии
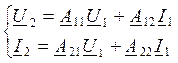
Zвх2=U2/I2
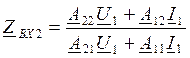
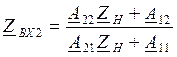
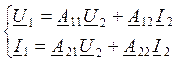
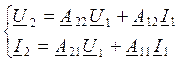
Замкнем 2 и 2`.
Z1K=A12/A22 – сопротивление первичных зажимов при замкнутых вторичных
Разомкнем 1 и 1`.
Z1Х=A11/A21 – входное сопротивление 4хполюсника со стороны 1х при разомкнутых 2`.
Z2Х=A12/A11, Z2Х=A22/A21
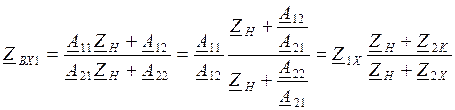
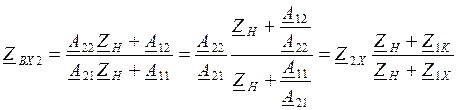
Входные сопротивления 4хполюсников иллюстрируют одно из свойств 4хполюсников трансформировать сопротивление. Кроме систем параметров, входящих в уравнения передачи 4хполюсников используется еще так называемые характеристические параметры. Это 2 характеристических сопротивления и характеристическая (собственная) постоянная передачи 4хполюсника.
ZС1, ZС2 такие, что если подключить к выходным зажимам в качестве нагрузки ZС2, то входное сопротивление со стороны входных зажимов будет ZС1. Если в качестве нагрузки будет ZС1, то входное сопротивление со стороны выходных зажимов будет ZС2.
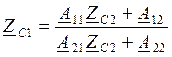
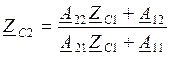
ZС1, ZС2 – неизвестные
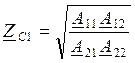
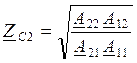
![]()
![]()
Если 4хполюсник симметричен, характеристические параметры одинаковые, что со стороны входных, что и со стороны выходных.
А11=А22, ZC1=ZC2=ZC
24. Собственная постоянная передачи четырехполюсника. Собственное ослабление. Собственная фазовая постоянная.
Собственная постоянная передачи 4хполюсника это комплексная величина и вводится для учета потери мощности в 4хполюснике в условиях согласованного режима.
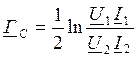 при ZГ=ZC1, ZH=ZC2
при ZГ=ZC1, ZH=ZC2
U1=I1ZC1, U2=I2ZC2
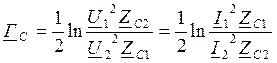
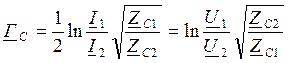
ZC1=ZC2=ZC
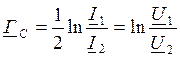
![]()
![]()
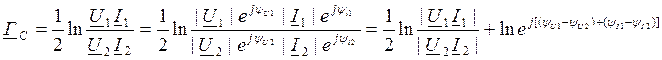
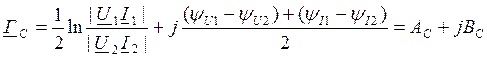
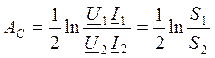 -
характеристическое сопротивление 4хполюсника
-
характеристическое сопротивление 4хполюсника
Эта величина показывает в логарифмическом масштабе, насколько изменится мощность на выходе 4хполюсника по сравнению с мощностью на входе в согласованном режиме работы.
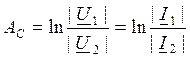
Единицы измерения отношения величин в масштабе натуральных логарифмов называется Нэппером (Нп). Ослабление в 1Нп соответствует отношению мощности в е2 раз. 1Нп=е2=7,39.
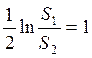 ,
, 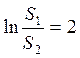 ,
, 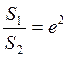
В симметричном 4хполюснике ослаблению в 1Нп соответствует уменьшение напряжения или тока в е=2,718 раз.
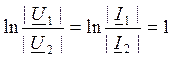 ,
, 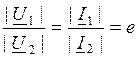
На практике используется не Нп, а Беллы. 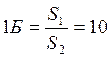 , 2Б=100,
, 2Б=100,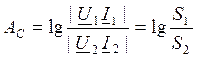
Эта величина довольно крупная и используется 0,1 величина – дБ.
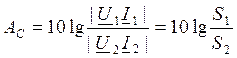
1Нп=8,7дБ, 1дБ=0,115Нп.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.