Синтезировать 4хполюсник значит построить его
схему. Синтез осуществляется по одной заданной характеристике. Требуемая
характеристика на практике задается в виде графика и поэтому на 1м этапе
синтеза требуется получить ее аналитическое выражение, т.е. решить задачу
аппроксимации. Не всякой полученной функции можно сопоставить электрическую
цепь. Поэтому необходимо обеспечить условие физической реализации цепей. Для
этого функция должна обладать всеми вышеперечисленными свойствами. Затем
решается задача реализации, т.е. составить схему цепи и определяются параметры
ее элементов. Из выражения для АЧХ 
и 
видно, что они зависят от большого
числа коэффициентов b0÷bm, а0÷аn,(для АЧХ), d0÷dm, c0÷cn,(для
АЧХ2).
1) метод Тейлора.
Основан, чтобы аппроксимирующая функция F(x) и N-1 ее производных совпадали со значением аппроксимируемой функции выбранной точки.
N – число искомых параметров
Пример: Представить уравнение f(x)=sinx линейной функции F(x)=a0+a1х в точке х=0.
f(x) – аппроксимируемая функция
F(x) - аппроксимирующая а) F(x)=f(x), a0+a1х=sinx, х=0, а0=0
б) F`(x)=f`(x), a1=cosx, х=0, а0=1
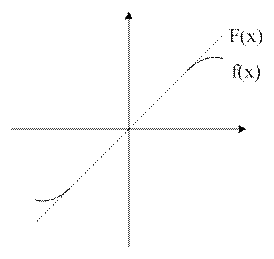
2) метод Чебышева.
Этот вид аппроксимации основан на отыскании таких коэф в полиноме, приближенно описывающих известную передаточную характеристику 4хполюсника, при которой его график отклонялся бы от нее наибольшим образом. Отклонение аппроксимирующей функции F(x) от f(x) должно быть минимальным. Согласно теории Чебышева F(x) на интервале приближения (-1; 1) f(x) будет меняться не менее чем (N+1) раз. n – степень полинома F(x), при этом отклонение будет чередоваться
Р(х)=F(x)-f(x) – полином Чебышева, n=4, n+1=5.
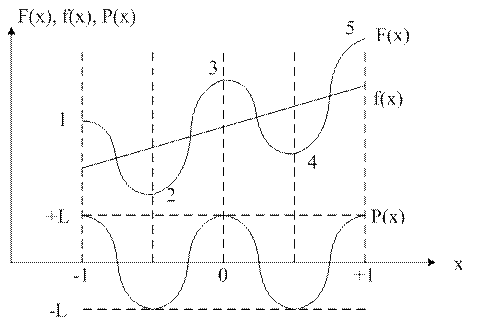
Если аппроксимирующая функция F(x) отклоняется 5 раз и знаки отклонения меняются.
Pn(x) имеет колебательный характер, поэтому может быть описан Pn(x)=cosnarccosx
n=0 P0(x)=1
n=1 P1(x)=x
n=2 P2(x)=2x2-1
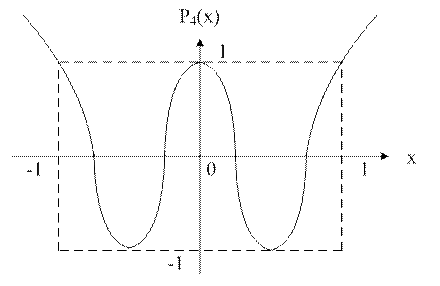
n=3 P3(x)=4x3-3x
…………………..
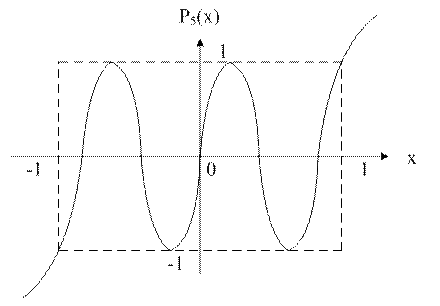
n≥2 Pn(x)=2xPn-1(x)-Pn-2(x)
P(x)=cosnarccosx
Pn(x)=chnArchx
29. Определение и классификация электрических фильтров. Полиномиальные фильтры.
Электрические фильтром называется 4хполюсник, пропускающий с малым ослаблением колебаний определенных частот и большим ослаблением колебаний других частот. Область частот в которой ослабление мало называется ПП. Область, в которой велико – полосой задерживания (ПЗ). Между этими полосами располагается так называемая промежуточная область (ПО). По расположению ПП на шкале частот различают: ФНЧ, ФВЧ, ПФ…
1) ФНЧ. ПП в области НЧ.
2) ФВЧ. ПП в области ВЧ.
3) ПФ. ПП в области СЧ.
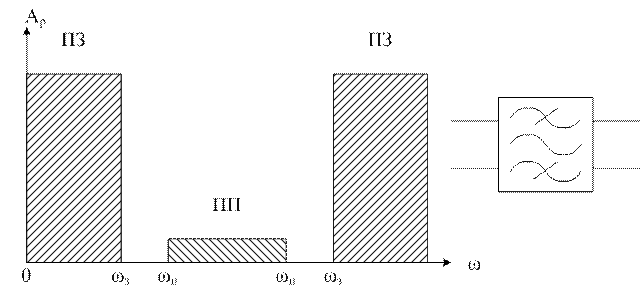
4) РФ. ПЗ в области СЧ.
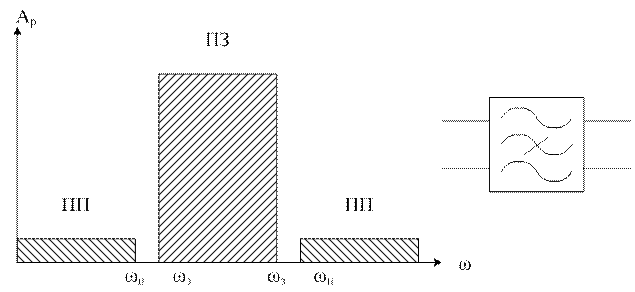
5) Многополосные фильтры.
В зависимости от используемой элементной базы выделилось несколько классов фильтров:
1) пассивные LC-фильтры.
2) активные RC.
3) цифровые фильтры.
4) ПЭФ.
5) магнитострикционные.
6) электромеханические.
7) фильтры с переключающимися конденсаторами.
8) фильтры на ПАВ.
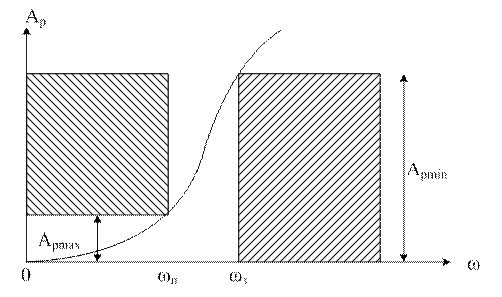
Под избирательностью понимается степень различия ПП и ПЗ или различий ослабления в этих полосах. Избирательность определяется крутизной характеристики рабочего ослабления. Чем > крутизна этой характеристики, тем сильнее ослабление в ПЗ, тем < уровень помех от подавляемых колебаний и тем лучше избирательность фильтров. Характеристики реальных фильтров отличаются от характеристик идеальных. Требования к характеристикам реальных задаются в виде допустимых пределов. Армакс – макс допустимое рабочее ослабление в ПП. Армин – мин-но допустимое рабочее ослабление в ПЗ. Требования к ослаблениям могут быть выражены.
Электрические фильтры с передаточной функцией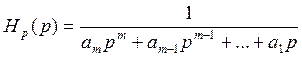 
называются полиномиальными. Заменив р
на jw получим КПФ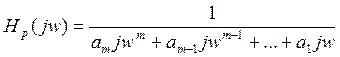 
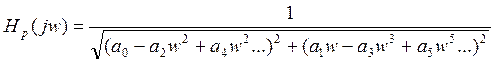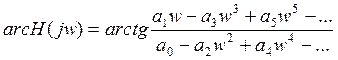- АЧХ
- ФЧХ
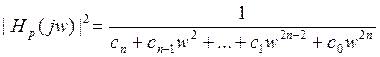- квадрат АЧХ
|Hp(jw)|2 и Ap(w) зависят от С0÷Сn и порядка фильтра и степени полинома n.
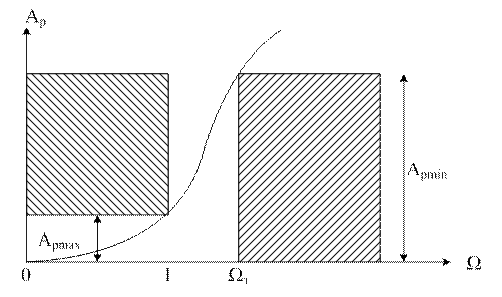
Имеет смысл подробно изучать и получать характеристики только ФНЧ. Характеристики других фильтров могут быть получены из характеристик ФНЧ с заменой переменной w. Эта замена называется преобразованием частоты.
30. Фильтры с характеристиками Баттерворта.
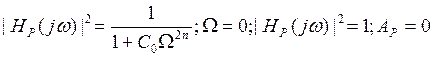
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.