Преобразование сигналов в нелинейных электрических цепях. Спектральная диаграмма воздействия на нелинейный элемент, страница 11

С ростом частоты квадрат АЧХ |H_p(jw)|² падает, а рабочее ослабление A_p увеличивается. A_p в ПП должно быть не > A_pмакс. Этому условию можно удовлетворить, если потребовать, чтобы на границе ПП Ω=1 A_p=A_pмакс.

A_p(Ω)=A_pмах, A_pмах=10lg(1+C₀), 0,1A_pмах=lg(1+C₀), 10^0,1Apмах=1+C₀, C₀=10^0,1Apмах-1, C₀=C², ε=√C₀, - коэф неравномерности

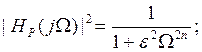 A_pмах=10lg(1+ε²Ω²ⁿ),

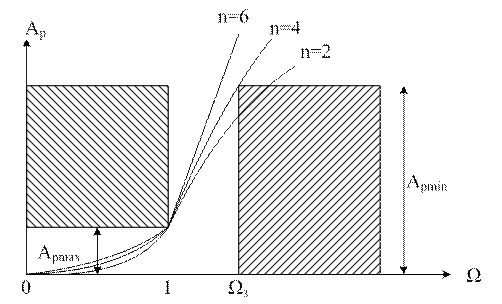
На границе ПЗ ослабление должно быть не < A_pмин. Для того чтобы удовлетворить это требование можно задаться выбором порядка фильтра.

A_p(Ω)=A_pмin, A_pмin=10lg(1+ε²Ω²ⁿ), A_pмin=10lg(1+ε²Ω₃²ⁿ), 0,1A_pмin=lg(1+ε²Ω₃²ⁿ), 10^0,1Apмin=1+ε²Ω₃²ⁿ,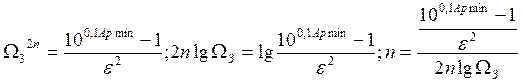

n – порядок фильтра

Полученное значение n округляется до ближайшего целого числа. Различия фильтров осуществляются по передаточным функциям. От ЧХ фильтра перейти к передаточной функции. Передаточную характеристику фильтров можно получить по ЧХ. Половина полюсов имеет вещественные отрицательные части и располагается в левой полуплоскости комплексной переменной Р, другая половина располагается зеркальным отображением первой. ИЗ полюсов, лежащих в левой полуплоскости комплексной переменной и формируется передаточная функция фильтра. 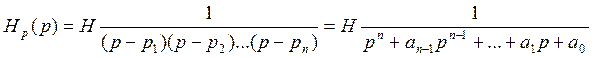; Н=1/ε

В_n(w)=Ωⁿ – полином Баттерворта

,

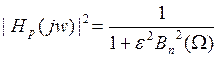Фильтры Баттерворта называются еще фильтрами с макс плоским нарастанием ослабления в ПП.

31. Фильтры с характеристиками Чебышева.

Характеристики фильтра Чебышева можно получить теми же формулами, но полином Баттерворта заменить на полином Чебышева.

,

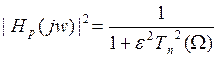Проанализируем на 2х первых шести полиномов Чебышева.

Т₀(Ω)=1

Т₁(Ω)=Ω

Т₂(Ω)=2Ω²-1

Т₃(Ω)=4Ω³-3Ω

Т₄(Ω)=8Ω⁴-8Ω²+1

Т₅(Ω)=16Ω⁵-20Ω³+5Ω

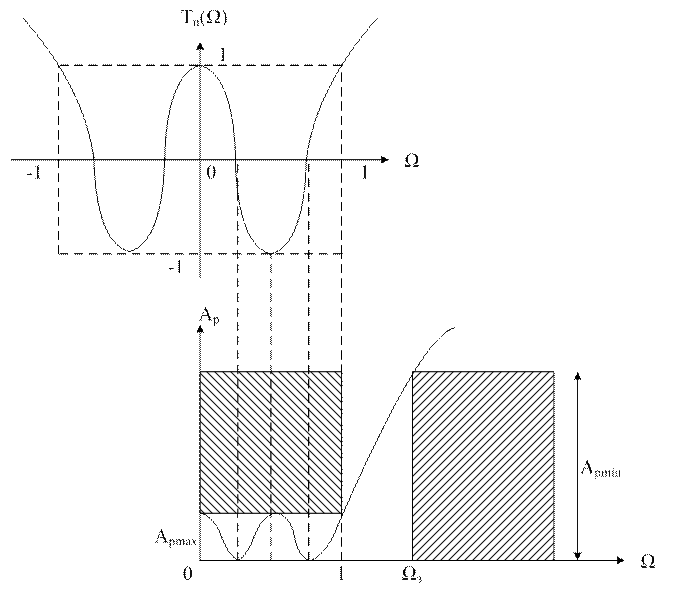
Начиная со 2го когда n≥2 Т_n(Ω)=2ΩT_n-1(Ω)-T_n-2(Ω). Это алгебраические формы записи. Существует еще и тригонометрические формы записи в пределах от -1 до 1.

Т_n(Ω)=cosnarccosΩ

Т₀(Ω)=cos0arccosΩ=1

Т₁(Ω)=cosarccosΩ=Ω

Т₂(Ω)=cos2arccosΩ=2cos²arccosΩ-1=2Ω²-1

За пределами этого интервала меньше 1 уравнение Чебышева представляется гиперболическими функциями. Т_n(Ω)=chnArchΩ. Анализ формул в интервале -1≤Ω≤1 показывает, что функция принимает значение «+1» или «-1» чередующиеся друг с другом. Вне интервала полином Чебышева монотонно возрастает. Пусть дан полином Чебы 4го порядка

Т_n(Ω)=0;

Т_n(Ω)=±1;

Эти фильтры еще наз-ся фильтры с равноволновой хар-кой ПЗ.

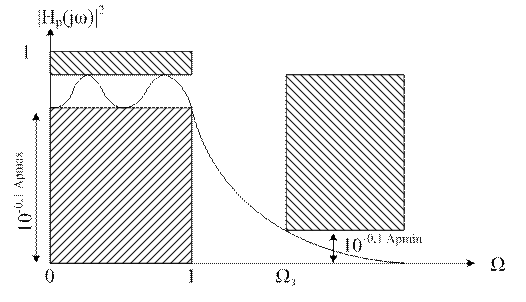
Выбрав ε мы обеспечили прохожд-е хар-ки. Требов-я к ПП выполнены.

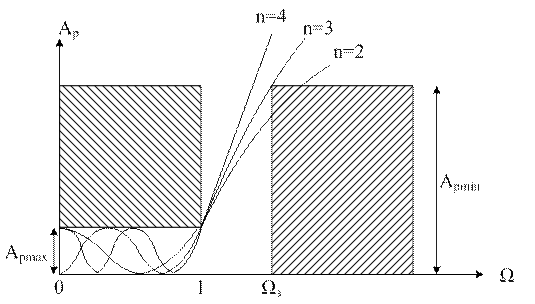
Рассм сем-во хар-к для ПЗ

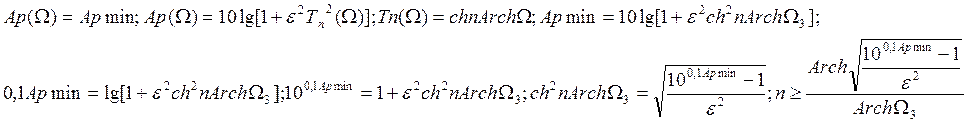Полученное значение округляется в большую сторону до целого числа.

Сравнение ЧХ фильтров Баттерворта и Чебышева показывает, что при одинаковых значениях n ослабление в ПЗ у Чебы значительно превышает ослабление фильтров Батт, т.е. при одних и тех же значениях можно обойтись меньшим порядком фильтра, но в ПП у Батт характеристика ослабления имеет монотонный характер и легче поддается корректировке при устранении искажений передаточных сигналов. У Чебы в ПП колебательный характер. Выбор типа полиномиального фильтра Баттерворта или Чебышева определяется конкретными условиями их применения в оборудовании связи.

32. Фильтры со всплесками ослабления Золотарева-Кауэра.

Если требуется малая ПО между ПП и ПЗ и большая величина ослабления порядок фильтра может оказаться слишком большим даже при использовании фильтра Чебышева. В этих случаях лучше применять фильтры со всплесками ослабления.

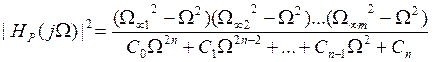
Ω_∞1, Ω_∞2,…, Ω_∞n, |H(jΩ)|² = 0

Ap(Ω) = ∞

Передаточная ф-ия таких фильтров имеет вид

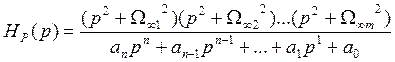
р₁, р₂, р_n – полюсы передаточной ф-ии.

р₀₁=±jΩ_∞1, р₀₂=±jΩ_∞2,…, р_0m=±jΩ_∞m – нули передаточной ф-ии.

Наибольшее распространение получили фильтры со всплеском ослабления на основе дробей Чебышева и Золотарева.

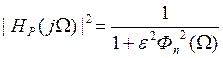
A_p(Ω)=10lg[1+ε²Ф_n²(φ)]

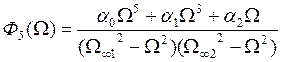
На частотах всплеска знаменатель →0, а дробь Чебышева →∞. Частным случаем дроби Чебышева является дробь Золотарева.

R_n(Ω) – дробь Золотарева.

A_p(Ω)=10lg[1+ε²R_n²(Ω)]

В ПЗ значение всех минимумов оказывается одиночными. Такие фильтры называются фильтрами с изоэкстремальными ослаблениями.

33. Реализация пассивных LC-фильтров нижних частот. Метод Дарлингтона.