Экономика и менеджмент \ Статистика

Выборочное наблюдение. Средние показатели деятельности заводов за 2008-2009 гг. Интегральная функция нормального распределения для определения коэффициента t, страница 7

k2       k1

1

2

3

4

5

5

0.569

0.669

0.764

0.806

0.835

6

0.500

0.632

0.704

0.751

0.785

7

0.444

0.575

0.651

0.702

0.739

8

0.399

0.527

0.604

0.657

0.697

9

0.362

0.488

0.563

0.618

0.659

10

0.332

0.451

0.527

0.582

0.624

12

0.283

0.394

0.466

0.521

0.564

14

0.247

0.348

0.417

0.471

0.514

16

0.219

0.312

0.378

0.429

0.477

18

0.197

0.283

0.345

0.394

0.435

20

0.179

0.259

0.318

0.364

0.404

Для приведенных расчетов:

Для пары факторовYиX

R2=0,8673     ν1=1,  ν2=15-2=13 

R2(крит)=(среднее между k2=12 и k2=14)=(0,283+0,247)/2=0,265

R2 > R2(крит) → 0.8673 > 0.265

Вывод:

С вероятностью р=1-α=1-0,05=0,95 можно утверждать, что связь между факторами «Стоимость основных фондов» и «Стоимость выпущенной продукции»  не случайная и существенная.

Для пары факторовYиZ

R2=0,1405     ν1=1,  ν2=15-2=13 

R2(крит)=(среднее между k2=12 и k2=14)=(0,283+0,247)/2=0,265

R2 < R2(крит) → 0.1405 < 0.265

Вывод:

С вероятностью р=1-α=1-0,05=0,95 можно утверждать, что связь между факторами «Стоимость основных фондов» и «Среднегодовая численность персонала» случайная и несущественная. 

ІІ. Ранговая корреляция

Как правило, коэффициент ранговой корреляции применяется для оценки взаимосвязи между признаками, один из которых или оба выражены качественно, например на основе экспертных оценок, баллов, результатов опроса и пр.

Примером такого представления данных может быть:

·  курс валюты (в грн/долл) в зависимости от политической ситуации в стране (балл);

·  уровень выполнения дипломных работ  (балл) в зависимости от научного обеспечения ВУЗа (экспертная оценка) и т.п.

Ранг числа Ri представляет собой число натурального ряда, которое показывает место данного показателя  по возрастанию или спаданию его значения в массиве наблюдений.

Тогда оценка взаимосвязи между признаками на основе их рангов проводится с помощью коэффициента ранговой корреляции Спирмена:


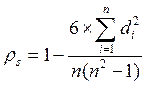
где  di= Rki-Rmi – разность рангов между показателями k и m;

n- объем выборки.

Коэффициент ранговой корреляции Спирмена принимает значения в границах от -1 до 1, по его знаку и величине судят о взаимосвязи признаков и ее направленности.

1.  Ранжирование пар признаков Y=f(X) и Y=f(Z) по возрастанию показателей.

Присвоение рангов показателям в массиве  целесообразно проводить, используя встроенную в MS Excel функцию «=РАНГ(число;ссылка;порядок)»*

Ранжирование показателей Y=f(X) 

Табл.6.

Скачать файл