Экономика и менеджмент \ Статистика

Выборочное наблюдение. Средние показатели деятельности заводов за 2008-2009 гг. Интегральная функция нормального распределения для определения коэффициента t, страница 16

Выбор наиболее достоверного тренда для сглаживания производится с помощью  функции в MS Excel «Добавить линию тренда»  и  следующей последовательности действий:

«– тип тренда –параметры – показывать уравнение на диаграмме – поместить на диаграмму величину достоверности аппроксимации R2».

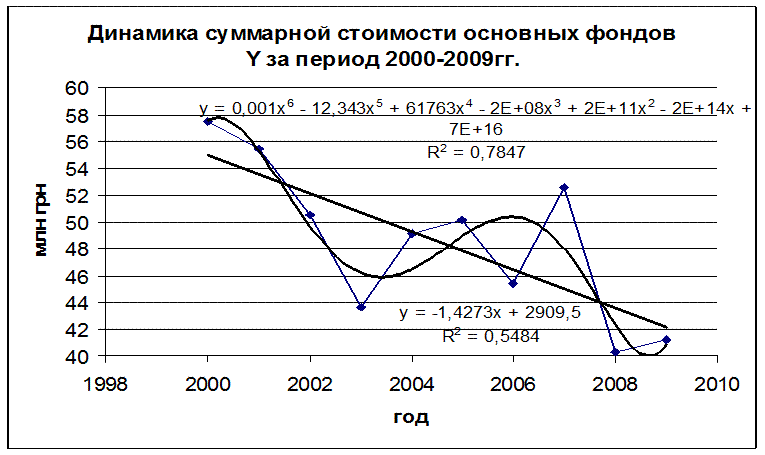
Как показал перебор функций тренда, максимально достоверно можно описать динамику стоимости основных фондов  с помощью полиномиальной функции 6-й степени (достоверность аппроксимации R2=78,5%). К примеру линейная функция дает точность аппроксимации всего 54,8%

2. Сглаживание  динамики признака XΣt с помощью метода скользящих средних.

Для анализа динамики признака необходимо построить график динамики ХΣt  за период 2000-2009гг.

Сглаживание с помощью метода скользящих средних производится с помощью  функции в MS Excel «Добавить линию тренда»  и  следующей последовательности действий:

«– тип тренда –линейная фильтрация - точки (указать количество точек для расчета среднего)».

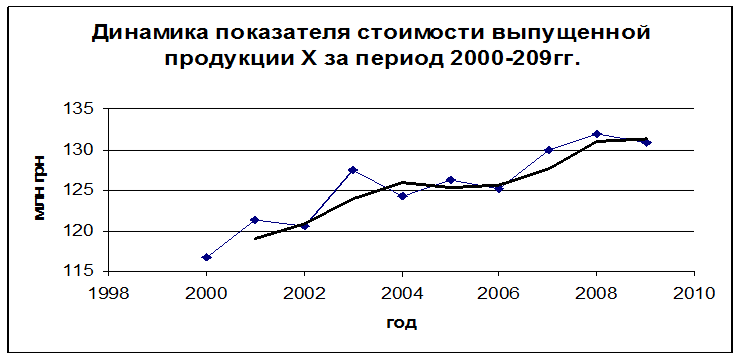
Как видно из рисунка, динамика стоимости выпущенной продукции (СВП) имеет позитивный тренд с двумя максимума  в 2004 и 2008 году. Это может говорить о наличии в ряду данных СВП цикличности с периодом 4 года.    

3. Определение индекса сезонности для  динамики признака ZΣt  .

Индекс сезонности рассчитывается по формуле:

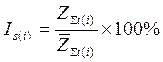
Индексы сезонности признака ZΣt

Табл.12

Год

Среднегодовая  численность персонала (чел.)

Среднее значение,

 (чел)

Индекс

Сезонності

(отн ед.)

ZΣt

Is(i)

2000

1951

1922

1,015*

2001

1800

0,937

2002

1773

0,922

2003

1812

0,943

2004

1946

1,012

2005

2020

1,051

2006

2035

1,059

2007

2013

1,047

2008

1950

1,015

2009

1920

0,999

* 1951/1922=1.015; 1800/1922=0,937 и т.д.

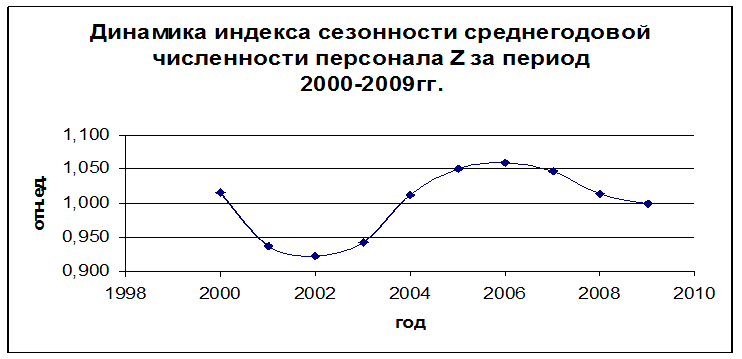
Динамика индекса сезонности показывает, что в ряду наблюдается периодичность – чередование минимумов (2002г) и максимумов (2006г). Можно говорить о цикличности изменения численности персонала  на указанной группе предприятий с периодом около 4-х лет.

ІІІ. Аналитическое выравнивание динамических рядов.

1. Аналитическое выравнивание признака YΣt(i) с помощью линейной функции.

Изобразим динамику показателя YΣt(i)  графически

Для аналитического выравнивания используем линейную функцию  вида:

YΣt(i) =b0+b1ti

где b0 и b1 –  неизвестные параметры модели

ti– время, год

Определение параметров линейной модели производится с помощью одношагового метода наименьших квадратов (1МНК) (см. тема 5, «Сглаживание и аналитическое выравнивание динамических рядов»).

«Наилучшие» среди всех возможных для исходной  базы данных параметры модели b0 и b1 определяются из системы нормальных уравнений (СНУ) для линейной модели:

Упростить  СНУ  можно с помощью  условного времени tусл(i) так, чтобы его сумма была равна нулю -  ∑ tусл(i)=0.  При этом среднему уровню ряда присваивается значение  tусл(i)=0, а остальным уровням реального времени присваиваются натуральные числа 1,2,……., n/2    и -1, -2, ……, -n/2.

Замечание: если число уровней ряда четное, то двум средним значениям ряда присваиваются условное время -1 и 1, а остальные уровни перенумеровываются последовательно до ± n/2.

Условное время

Табл.13

Скачать файл