Выборочное наблюдение. Средние показатели деятельности заводов за 2008-2009 гг. Интегральная функция нормального распределения для определения коэффициента t, страница 5

Тогда 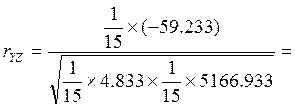  -0,37182

Аналогичный результат получим с помощью функции «=КОРРЕЛ(массивY;массивZ)».   

Вывод:

Значение коэффициента корреляции r_YZ=-0.37182 указывает:

·  знак  « - » на наличие  обратной связи;

·  величина 0,37182 на умеренную (стремящуюся к средней) связь между признаками “Стоимость основных фондов» и «Среднегодовая численность персонала».               

3. Проверка значимости коэффициентов корреляции с помощью критерия Стьюдента t_r

Критерий Стьюдента t_r  для пар факторов рассчитывается по формуле:

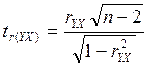
где r_YX     и  r_YZ  - коэффициенты корреляции Пирсона для соответствующих пар факторов;

n  - объем выборки.

Тогда t-тест Стьюдента

·  для пары факторовYиX:

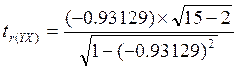  =-9,2175  

·  для пары факторовYиX:

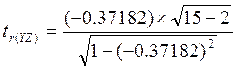  =-1,4577    

Расчетное абсолютное значение критерия  Стьюдента сравнивают с критическим (табличным) для заданного числа степеней свободы ν=n-2.

Критические значения t-критерия Стьюдента  для уровня существенности α=0,05

Табл.4.1.