Погрешность позиционирования промышленного робота. Первичные ошибки. Погрешности обобщенных координат, страница 9

Если ввести обозначения

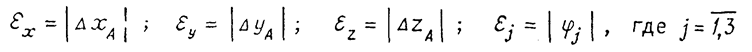
и предположить наиболее неблагоприятное сочетание для j_j , то получаем ограничения на погрешность позиционирования:

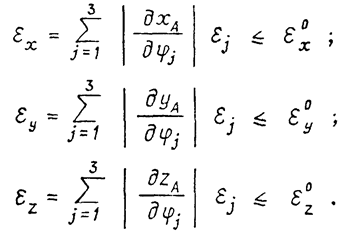                               (4)

Конкретно для рассматриваемой схемы имеем

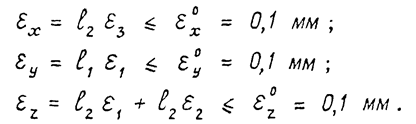                               (5)

Считая в первом приближении стоимости обеспечения единичных точностей равноценными, будем разыскивать минимум функции стоимости изготовления МС:

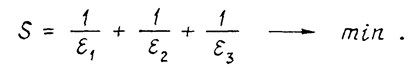                               (6)

Таким образом, необходимо найти решение задачи выпуклого программирования для функции качества (6) с ограничениями на погрешность позиционирования (5) и естественными ограничениями положительной определенности параметров e_j:

                                          (7)

В соотношениях (5) погрешность e₃,  с погрешностями e₁и e₂ не связана. Поэтому из задачи (5)...(7) можно выделить две независимых части:

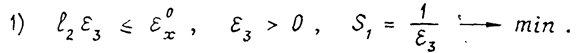             (8)

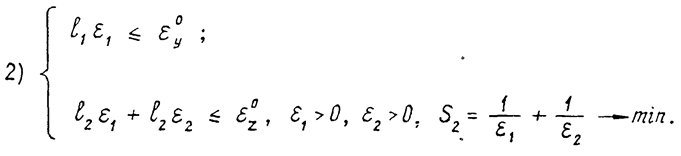       (9)

Задача в постановке (8) имеет простое решение:

e₃=e_х⁰/l₂=0,1/300=0,00033(рад)

Для решения задачи (9) изобразим область допустимых решений в плоскости e₁e₂ (рис.3).

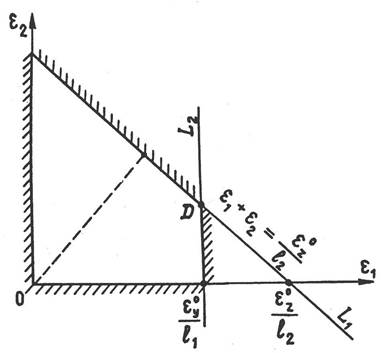
Рис.3. Область допустимых значений при точностном синтезе

Поскольку решение задачи может располагаться только на границе, то для его отыскания аналитическим способом следует:

1) последовательно рассмотреть поведение функции S₂ на каждой границе L₁, L₂  (исключая границы  e_j= 0);

2) найти минимумы S₂ на этих границах в пределах отрезков, заключенных между точками пересечения прямых L₁, L₂ с осями координат и точкой  D;

3) сравнить минимумы между собой и выбрать предпочтительное решение.

В результате выполнения этих операций получаем:

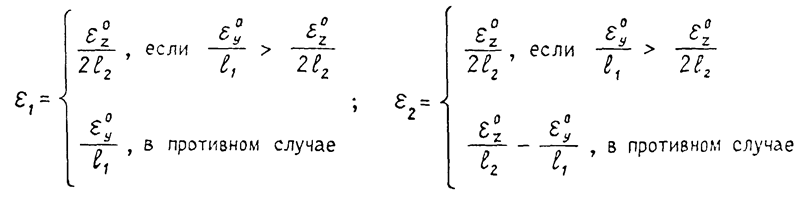
откуда

e₁= 0,00017 рад; e₂ = 0,00017 рад.

Дадим теперь приближенную оценку жесткостных параметров наиболее ответственных узлов конструкции робота «Ритм-01.01». Параметры сечения руки с массой груза на конце  т₀ = 0,1 кг  определим по схеме на рис.4а, полагая для простоты руку однородной и прямолинейной, а силу тяжести звена сосредоточенной в его центре.

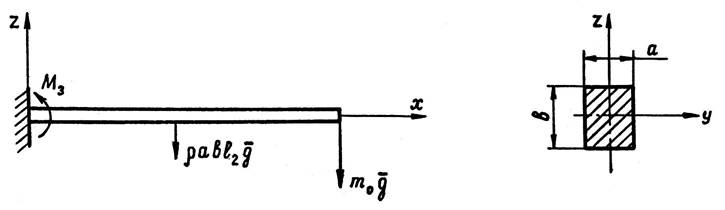
а)

       

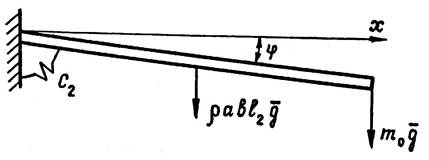
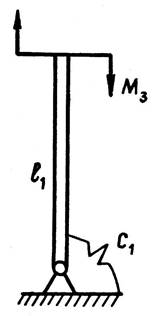
      б)                                                           в)

Рис.4. Схема жесткостного синтеза звеньев МС:

а,б – руки; в – стойки

В силу линейности используемой теории деформируемой балки решение задачи изгиба можно вести посредством суперпозиции перемещений  W₁ , W₂   в точках оси  х  от двух сосредоточенных в них сил:

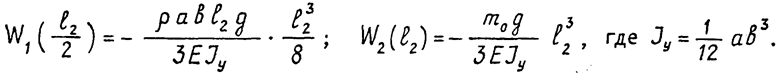
В схеме с сосредоточенной жесткостью (рис.4б) этим двум значениям перемещений соответствуют различные углы поворота звена вокруг оси  Оу:

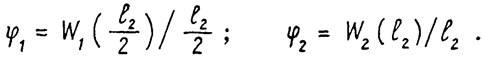
Тогда суммарный угол составляет величину:

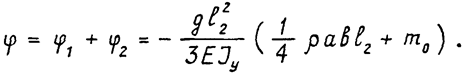
Жесткость руки будет достаточна, если ½j½£e₂  или:

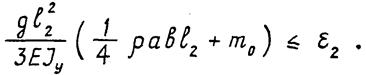
Принимая для определенности b= 2а, получаем, что минимальное значение а , обеспечивающее требуемую жесткость руки, может быть найдено из уравнения:

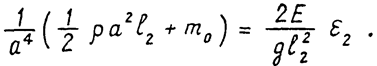
Подставляя для стали  r= 7800 кг*м^-3, Е = 2,1.10¹¹   Н*м^-2, имеем  а³6,6 мм. Принимаем  a = 7 мм,  b = 14 мм. Эти размеры сечения звена хорошо согласуются с действительными. Следовательно, жесткость руки робота «Ритм-01.01» на изгиб можно считать достаточной.

Коэффициент жесткости  С₂  (рис.4б) может быть рассчитан из соотношения:

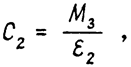
где  М₃ – момент заделки балки на рис.4а.

В нашем случае величина М₃ равна:

Для оценки минимального коэффициента жесткости  С₁ (рис.2) обратимся к расчетной схеме на рис.4в, в соответствии с которой

16 проектированиЕ РТС

16.1 Постановка задачи проектирования РТС

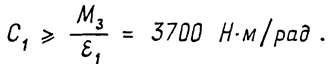
Проектирование роботизированного производства можно разделить на два этапа.

Первый этап: на основе технико-экономического анализа производства выбирают объекты роботизации, необходимый состав основного технологического оборудования и последовательность обработки на нем изделий.

После проведения первого этапа можно получить информацию (исходные данные) для второго этапа – непосредственного проектирования РТК:

об изделиях, подлежащих обработке на РТК: размерах и форме изделия, его массе, жесткости, прочности, магнитных свойствах и т. п.;

о технологическом оборудовании: его составе j (j=1, 2, ..., J -порядковые номера оборудования), форме и размерах;