Погрешность позиционирования промышленного робота. Первичные ошибки. Погрешности обобщенных координат, страница 4

Каждое звено МС соединяется со смежными посредством кинематической пары. Проведем через центры кинематических пар звена i ось х_i  (рис.1) и свяжем с каждым звеном систему координат  o_i х_iу_i z_i. Пространственное тело имеет шесть степеней свободы. Этим степеням свободы соответствуют шесть  составляющих погрешности позиционирования звена. Каждая составляющая погрешности позиционирования и ориентирования звена может быть объяснена не идеальностью соответствующих жесткостных характеристик.

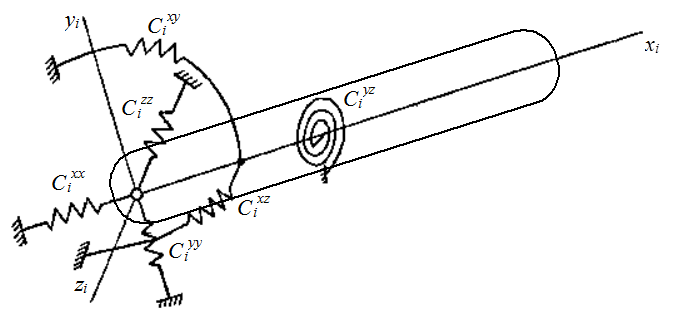
Рис.1. Составляющие погрешности типового звена манипулятора ПР

Таким образом, три составляющих погрешности позиционирования e_i^xx, e_i^yy,e_i^zz и три составляющих погрешности ориентирования e_i^xy, e_i^xz, e_i^yz  звена iобуславливаются шестью коэффициентами жесткости: тремя отвечающими за поступательное перемещение (или удлинение в соответствующем направлении) звена i (С_i^xx, С_i^yy, С_i^zz) и тремя, отвечающими за повороты (или изгибы и кручения) звена i (С_i^xy^, С_i^yz, С_i^xz).

В точке А  рабочей зоны конфигурация ={q₁,...,q_n}|_A определена посредством решения обратной задачи о положении МС. Решение прямой задачи о положении на малых перемещениях e_i^j при конфигурации  позволяет однозначно связать набор составляющих погрешностей позиционирования всех звеньев

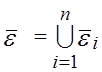;         ={e_i^xx, e_i^yy, e_i^zz ,e_i^xy, e_i^xz, e_i^yz}

с набором составляющих погрешностей позиционирования и ориентирования схвата в точке А

={e_A^xx, e_A^yy, e_A^zz ,e_A^xy, e_A^xz, e_A^yz}

Решение задачи статики для МС в конфигурации  позволяет связать вектор  с вектором

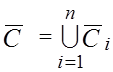;      ={C_i^xx, C_i^yy, C_i^zz ,C_i^xy, C_i^xz, C_i^yz}={C_i^j}

Если при этом удается вычислить определенный показатель качества МС (стоимость, масса, показатели инерционности и др.)

К=К (),

то задача проектирования жесткости может быть записана формально так: найти экстремум функции качества

К ()®ехtr (1)

при условиях

e_A^j()£e_A^jo    (j=1,6) (2)

C_i^j>0    (j=1,6, i=1,n) (3)

Решением задачи (1)–(3) служит набор компонентов вектора , характеризующих жесткость МС и обеспечивающих требуемую точность позиционирования и ориентации  e_A^jo  в точке А наилучшим образом в смысле качества К.

Максимальное число параметров оптимизации в задаче равно 6n, поэтому уже при n > 2 поиск экстремума требует больших затрат времени и становится мало эффективным.

14.2 Декомпозиция задачи проектирования МС. Оптимизация точности МС

В большинстве случаев используются методы декомпозиции оптимизационной задачи большой размерности и представления ее в виде двухуровневой модели:

– на верхнем уровне оптимизации назначаются укрупненные параметры для подсистем в соответствии с критерием оптимизации верхнего уровня;

– на нижнем уровне укрупненные параметры выступают в форме ограничений для соответствующих подсистем.

Оптимизация внутри каждой подсистемы ведется независимо от других, но по критериям, согласованным (не противоречащим) критерию верхнего уровня. На каждом шаге оптимизации значения функций качества подсистем нижнего уровня пересчитываются к значению функции качества верхнего уровня и итерация повторяется.

Декомпозировать задачу (1)–(3) можно следующим образом. На верхнем уровне двухуровневого процесса производится распределение погрешности  по степеням подвижности, то есть разыскиваются наборы , (i=1,n) такие, что в точке А  выполняется требование

e_A^j() £e_A^jo    (j=1,6,  i=1,n)   (4)

причем при наименьшем значении критерия качества

K₁() ® min,                 (5)

который условно назовем стоимостью.

Если точность звена характеризовать величиной, обратной погрешности (1/e_i^j), и условиться, что достижение единичной точности по степени свободы j звена i обходится в затраты Р_i^j, то функция

K₁()=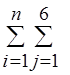(Р_i^j/e_i^j)     (6)

характеризует стоимость МС, обладающей по каждому звену максимальной погрешностью.

Величина e_i^j/Р_i^j является обратной по отношению к стоимости обеспечения погрешности  e_i^j  по степени свободы j звена i. Каждое такое отношение можно рассматривать как частный критерий, который следует устремлять к максимуму. Для учета всех частных критериев в одном общем можно составить аддитивный критерий вида