Погрешность позиционирования промышленного робота. Первичные ошибки. Погрешности обобщенных координат, страница 7

С_з^yz »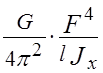, (17)

при изгибах

С_з^xz»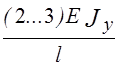 ,    С_з^xy»  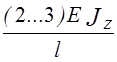 .      (18)

Значение численного коэффициента в двух последних формулах зависит от схемы нагружения балки. Так, при изгибе балки моментом этот коэффициент равен 2, перерезывающей силой - 3. Различные комбинированные варианты дают промежуточные значения.

Итак, пара независимых параметров  R,  F_o  (или а , b) определяет четыре коэффициента жесткости несущей конструкции звена, что снижает размерность задачи оптимизации. Результатом синтеза жесткости с использованием идеализированной конструкции является определение параметров  R ,  F_o , значений осевых моментов инерции сечений  J_xo = R²F_o ; J_yo  = J_zo = 0,5 R²F_o , a также коэффициентов жесткости звена.

Реальная конфигурация профиля поперечного сечения может отличаться от рассмотренных. Тогда параметры сечения выбранного профиля могут быть подобраны из условий:

J_x ³ J_xo ; J_y ³ J_yo ; J_z ³ J_zo.        (19)

но удобнее для этой цели пользоваться коэффициентами унификации характеристик конструкции. Под коэффициентом унификации определенной характеристики конструкции понимают отношение  значения этой характеристики для реальной конструкции к значению соответствующей характеристики идеализированной конструкции. Для произвольной балки можно указать три таких коэффициента:

K_x = J_x / J_xo ; K_y = J_y / J_yo ; K_z = J_z / J_zo .(20)

Выражения этих коэффициентов через параметры реальной и идеализированной конструкций для ряда возможных профилей приведены в табл.1.

При оценке массы и коэффициентов жесткости механической передачи исходим из предположения, что тип редуктора известен. Масса редуктора в первую очередь определяется такими факторами, как коэффициент редукции  i  и максимальный передаваемый момент, приведенный к валу звена:

т_p =  f (M, i) .                 (21)

Такого рода зависимость следует получать эмпирическим путем посредством обработки статистических данных для редукторов рассматриваемого типа. При обработке статистических данных можно предположить прямую пропорциональность между массой редуктора и передаваемым моментом, а также прямую зависимость массы от числа ступеней редукции, которое приближенно можно оценить как    k' ln i . Таким образом, представляется удобным аппроксимировать статистические данные зависимостью вида:

т_p = k М lп i = k_pМ ,        (21а)

где  k_p= k ln i  ;   k – коэффициент аппроксимации.

Жесткость механической передачи можно в первом приближении считать пропорциональной его массе, то есть полагать

С_p = l_pМ .                      (22)

Распределение массы редуктора по звену (звеньям) МС зависит как от компоновочно-кинематической схемы, так и от типа редуктора. Однако, при распределении масс следует руководствоваться наиболее простыми рабочими гипотезами.

Массу двигателя следует также искать в прямой зависимости от максимального нагрузочного момента,что при приведении к валу двигателя дает

m_д=k_д i M,              (23)

где  k_д  определяется для заданного тина двигателя на основе обработки статистических данных, получаемых из справочников. Массы датчиков положения и скорости от величины М  можно считать не зависящими: эти элементы выбираются из кинематических характеристик и соображений не механического плана.

Коэффициент жесткости механической передачи  C_p вносит вклад в ту составляющую жесткости, за которую отвечает кинематическая пара соответствующей степени подвижности: это C_p^xx, C_p^yy, C_p^zz при поступательных парах,  C_p^yz  при ротации, C_p^xz, C_p^xy – при вращательных парах.