![]() (7)
(7)
где rc' - радиус-вектор центра С' рабочего органа реального ИУ, мм; Δli - первичная ошибка длины i-гo звена, мм; Δqj -погрешность j-й обобщенной координаты, рад.
Разложим функцию положения реального исполнительного устройства в ряд Тейлора:
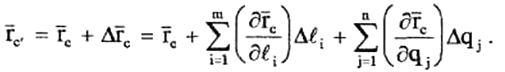 (8)
(8)
Вычитаем из разложенной в ряд Тейлора функции положения (8) реального исполнительного устройства функцию положения (6) теоретической схемы ИУ. Получим вектор полной погрешности позиционирования промышленного робота, мм:
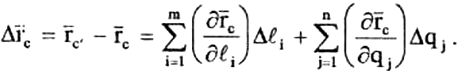 (9)
(9)
С учетом зависимости (1)
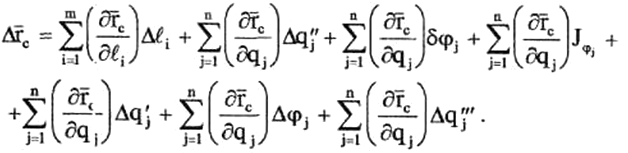 (10)
(10)
Проектируя вектор полной погрешности позиционирования ПР на координатные оси X, У и Z, получим погрешности позиционирования вдоль этих осей:
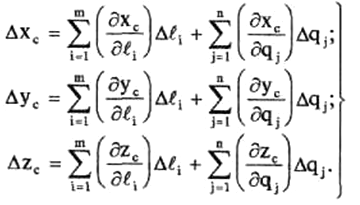 (11)
(11)
Полная погрешность позиционирования ПР равна, мм:
![]() (12)
(12)
Направление перемещения точки С можно характеризовать углами α и β, град, (рис.6), равными:
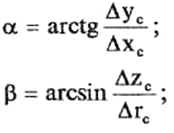 (13)
(13) 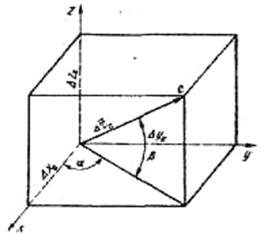
Рис.6
Вследствие наличия первичных ошибок и погрешностей обобщенных координат в действительном механизме значения его передаточных функций также будут иметь ошибки.
Запишем погрешность функции положения (погрешность позиционирования) рабочего органа исполнительного устройства ПР в общем виде (рис.7):
![]()
где rд - радиус-вектор (функция положения) рабочего органа действительного исполнительного устройства; rо - радиус-вектор (функция положения) рабочего органа теоретического исполнительного устройства.
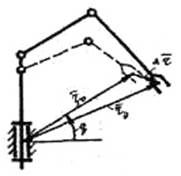
Рис.7
Ошибка первой передаточной функции (аналог скорости) будет равна:
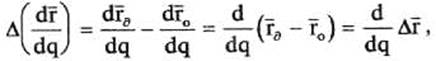
где q - обобщенная координата, определяющая положение радиус-вектора rо рабочего органа теоретического исполнительного устройства относительно стойки (основания).
Ошибка второй передаточной функции (аналога ускорения):
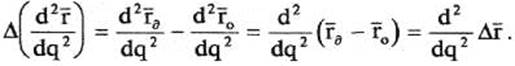
Из-за наличия ошибок передаточных функций скорости и ускорения звеньев действительного исполнительного устройства будут иметь ошибки.
Ошибка скорости рабочего органа:
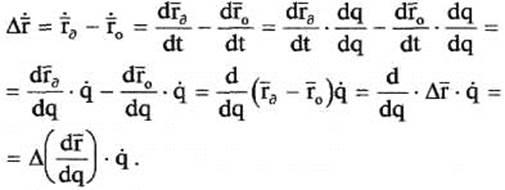 (14)
(14)
Ошибка ускорения рабочего органа:
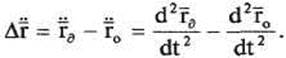
Найдем вторую производную:
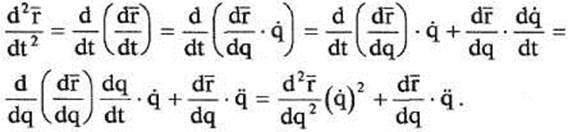
Таким образом, ошибка ускорения окончательно будет равна:
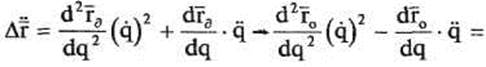
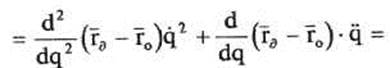
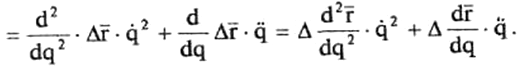 (15)
(15)
Наличие ошибок ускорения приводит к возникновению в исполнительном устройстве дополнительных сил инерции и соответствующих им реактивных сил в кинематических парах.
Точностные показатели промышленного робота (ПР) определяющим образом зависят от жесткости механической системы манипулятора ПР. Вместе с тем, одна и та же точность может достигаться при различных наборах жесткостных параметров манипуляционной системы (МС). Это предоставляет возможность выбора оптимального набора жесткостных параметров из множества допустимых при заданной точности. В качестве критерия оптимальности можно принимать такие функции качества, как стоимость изготовления или эксплуатации МС, массо-инерционные показатели и другие.
Задача жесткостного проектирования возникает на этапе, когда уже определены кинематическая структура МС и ее геометрические размеры, выбрана конструктивно-компоновочная схема, обуславливаемая типом используемых механических передач и размещением исполнительных двигателей, определены грузоподъемность, точность ПР, выявлен набор точек позиционирования в рабочей зоне ПР, в которых требуется обеспечить заданную точность, выделены характерные траектории и законы движения ПР. Поскольку процесс проектирования ПР является итерационным, то на рассматриваемом шаге итерации предполагаются выбранными исполнительные двигатели и необходимый набор датчиков. Специфические особенности ПР как технической системы позволяют выделить три основные причины, обуславливающие не идеальность его жесткости:
1) упругость звеньев МС;
2) упругость механических передач;
3) конечная жесткость исполнительных приводов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.