Погрешность позиционирования промышленного робота. Первичные ошибки. Погрешности обобщенных координат, страница 5

K₁()=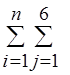(e_i^j/Р_i^j) ® max   (7)

Особенность этого критерия – линейность.

Решение задачи (4), (5) определяет максимально допустимые погрешности  e_i^j >0  для каждого звена. Выясним конкретный вид связи e_i^j c e_A^j . Обозначим через j_i^j  обобщенную координату, соответствующую максимальной погрешности e_i^j ; j_A^j  – координату, соответствующую погрешности e_A^j  и разложим j_A^j (j _i ^j) по степеням j_i^j в окрестности j_i^j = 0 , ограничиваясь в записи линейными членами:

j_A^j»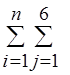(¶j_A^j/¶j_i^j)×j_i^j,     (j=1,6)

Наименее благоприятна ситуация, когда все слагаемые двойной суммы имеют один знак. Обозначая

|j_i^j|=e_i^j,     |j_A^j|=e_A^j, приходим к соотношениям:

e_A^j»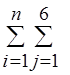(¶j_A^j/¶j_i^j)×e_i^j£e_A^jo,     (j=1,6)   (8)

Целевая функция (7) с линейными ограничениями (8) образуют задачу линейного программирования, для которой размерность 6n  не является большой.

Если же использовать в качестве целевой функции не взвешенный аддитивный критерий (7), а монотонную по любому направлению в евклидовом пространстве размерности 6n функцию (6), то приходим к задаче выпуклого программирования, для которой данную размерность также нельзя считать чрезмерно большой, поскольку экстремум расположен также на границе области, а область ограничена многогранником.

Решением задачи верхнего уровня – задачи точностного синтеза МC – назначается для каждого звена i шесть ограничений по погрешности позиционирования:

e_i^j()½_A £e_i ^jo  (j=1,6)   (9)

На нижнем уровне оптимизации проектируется жесткость звена, то есть определяются параметры жесткости

C_i^j >0    (j =1,6)             (10)

дающие экстремум функции качества

K₂() ® extr.   (11)

Это задача нелинейного программирования; ее размерность не более шести и поэтому она может быть эффективно решена с применением вычислительной техники.

После решения задачи проектирования жесткости звена  (9) – (11) для каждого i=1,n рассчитываются коэффициенты Р_i^j, вновь решается задача верхнего уровня, и т.д. до получения устойчивого решения.

При менее строгом подходе коэффициенты  Р_i^j могут быть получены посредством обработки статистического материала либо назначены проектировщиком на основе экспертных оценок. Тогда задача проектирования жесткости МС распадается на последовательность двух задач: задачу точностного синтеза МС и задачу проектирования жесткости для каждого звена.

Первая задача довольно подробно представлена соотношениями (6) – (8).

14.3 Синтез звеньев МС оптимальной жесткости

Решение задачи проектирования жесткости звеньев представляет большие трудности, чем задача  оптимизации точности МС. В этой связи наибольший интерес представляют два аспекта:

1) связь коэффициентов жесткости с погрешностью .позиционирования;

2) вычисление функции  качества.

Для выявления связис   необходимо решить задачу статики твердого тела  для звена  i, а, следовательно, знать распределение нагрузки по звену. При отбрасывании связей - смежных звеньев, их воздействия заменяем реакциями связей (рис. 2).

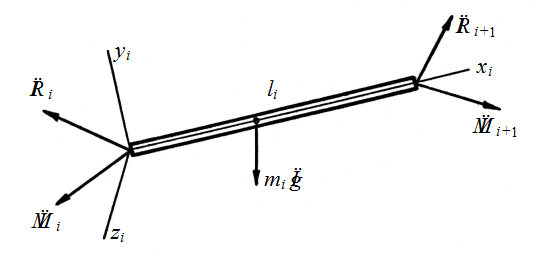
Рис.2. Схема сил, действующих на звено

Кроме реакций смежных звеньев звено нагружено силой тяжести m_ig¯ . Поскольку для звена i = n нагрузка на правом конце задана (это сила тяжести объекта манипулирования), то решать задачу следует в первую очередь для последнего звена и далее в последовательности от схвата к стойке. В результате определяются реакции  R¯  _i, M¯  _i, через которые и рассчитываются коэффициенты жесткости, поскольку

R_x = C^xxd ^xx, R_y = C^yyd ^yy, R_z = C^zzd ^zz,

M_x = C^yzj ^yz, M_y = C^xzj ^xz, M_z = C^xyj ^xy.  (12)

где  d ^xx, d ^yy, d ^zz – перемещения левого конца звена в направлении соответствующих осей, вызывающие соответствующие деформации пружин;  j^yz, j^xz, j^xy – величины закручивания пружин, отвечающих на повороты звена. Индекс i для краткости опущен.

Погрешности связаны с перемещениями зависимостями:

e ^xx=½d ^xx½, e ^yy=½d ^yy½, e ^zz=½d ^zz½

e ^xy=½j ^xy½, e ^xz=½j ^xz½,  e ^yz=½j ^yz½   (13)