Другие предметы \ Изыскания и проектирование железных дорог

Расчеты верхнего строения пути. Расчеты пути на прочность. Классификация рельсов по длине. Расчеты бесстыкового пути, страница 9

11)  за условный предел текучести [] рельсовой стали принимают напряжения растяжения, при котором образец d=10 мм и длиной 100 мм, вырезанный из верхней части головки, получат удлинение, равное 0,2%, или за условный предел текучести [] принимают результаты статических испытаний кусков рельсов на изгиб. Допускаемое напряжение изгиба в рельсах [], исходя из их работы на выносливость для незакаленных рельсов, равно 3500, объемнозакаленных, сталь которых раскисленна комплексными лигатурами – 4000 кгс/см2;

12)  продольные температурные силы непосредственно расчетной схемой не учитываются;

13)  вертикальные силы от расчетного колеса принимаются как максимально вероятные Ррасч, определяемые с уровнем вероятности их непревышения Ф=0,994 и Хф=2,5;

14)  влияние климатических факторов учитывается лишь при воздействиях на рельсы и изменениях жесткости пути (U, k) при промерзании шпал, балласта и земляного полотна;

15)  неупругие сопротивления не учитываются;

16)  максимальная сила инерции при проходе колесом изолированной неровности на пути уже после выхода колеса из неровности;

17)  подавляющая часть неровностей на колесах принимается в виде непрерывных, доля которых (1-q)=0,95. Считается, что остальная часть колес (q=5%) имеет изолированные неровности. Дисбаланс колес не учитывается.

Принимается, что прочность ВСП определяется, в первую очередь, прочностью рельсов по напряжениям изгиба. Превышение допускаемых напряжений в шпалах и балласте указывает на необходимость усиления пути, но не требует ограничения скорости движения  поездов. Превышение напряжений на основной площадке земляного полотна требует введения ограничения скорости движения  и усиления пути.

Динамический расчет пути под воздействием системы грузов сводится к тому, чтобы найти одну такую силу, которая, будучи статически приложенной в сечении 0, по своему воздействию на путь оказалась бы эквивалентной динамическому воздействию на это сечение пути всей системы грузов. Ввиду разницы в эпюрах μ и η эквивалентная сила для определения  изгибающего момента будет отличаться от эквивалентной силы  для определения упругого прогиба рельсов и давления на шпалы.

Из формулы (1.9) запишем, что

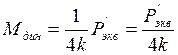,                                       (1.18)

так как в сечении 0 величина μ=1.

С учетом влияния горизонтальных поперечных сил предыдущая формула и формулы (1.10) и (1.12) принимают вид:

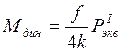,                                          (1.18а)

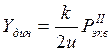,                                            (1.19)

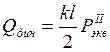.                                            (1.20)

Эквивалентные силы складываются из статического давления (остающимся постоянным) и переменных дополнительных сил воздействия на путь от работы  рессор, неровностей пути и неровностей на колесах, от неравноупругости рельсовых опор. Каждая из переменных сил имеет  определенное значение и максимальную возможную величину. Совпадение максимальных значений  всех составляющих переменных сил совершенно невероятно. Поэтому приходится использовать закономерности теории вероятностей и математической статистики.

3.2 Среднеквадратическое отклонение

3.2.1 Кривые распределения вероятностей

Положим, что мы имеем ряд частных значений х1, х2, … , хп. Среднее арифметическое этих величин 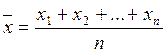. Чем больше n, тем точнее средняя величина характеризует изучаемый фактор. В двух случаях х1=900, х2=700 кгс/см2 и х1=1200, х2=400 – средние равны, но в первом случае напряжения достигали 900, а во втором – 1200 кгс/см2.

Измеритель 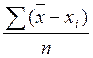 всегда равен нулю, поэтому для оценки степени рассеяния частных значений, или дисперсии, определить среднеквадратическое отклонение можно по следующей формуле:

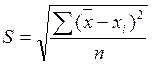
Величина под корнем называется дисперсией, следовательно, дисперсия равна S2.

Тензодатчиком определяются напряжения в рельсе от одного экипажа, пропущенного с одинаковой скоростью много раз. Полученные частные значения отличаются друг от друга, поскольку случайные комбинации переменных сил воздействия на путь складываются при каждом заезде по-разному.

Гистограмма распределения рис

Полигон распределения

Полигон частостей – в долях или %

С уменьшением интервала частных значений многоугольник частостей превратится в плавную кривую.

Экспериментально доказано, что сумма слагающих динамическую нагрузку колеса на рельс, по крайней мере в средней части графика распределения плотностей вероятностей, близка к закону распределения Гаусса или нормальному.

λ=0

Ф=0,5

S1=400, S2=500, S3=300

λ=1

Ф=0,841

λ=2

???

???

λ=2,5

???

λ=3

???

λ=6

Ф=1

,                                      (1.21)

Sp – среднеквадратическое отклонение дополнительного вертикального      воздействия на путь Рр от работы рессор;

Sнп – среднеквадратическое отклонение дополнительного инерционного вертикального усилия от неровности пути Рнп;

Sинк – среднеквадратическое отклонение дополнительного инерционного вертикального усилия на рельс Ринк от влияния изолированной неровности на колесе;

Sннк – среднеквадратическое отклонение дополнительного инерционного вертикального усилия на рельсы Рннк от влияния непрерывной неровности на колесе;

q – доля колес на поезде, имеющих изолированные неровности на колесе, принимаемая равной 0,05, т.е. считают, что остальная доля колес (0,95) имеет лишь непрерывные неровности на поверхности катания колес.

Основные расчетные формулы

Эквивалентная сила для изгибающего момента:

                                           (1.22)

для давления на шпалу и для прогиба

                                      (1.23)

где     Рср – сумма средних значений всех вертикальных сил от расчетного колеса;

Рср+2,5S – максимальное давление на рельс от расчетного колеса;

следовательно,

                                                             (1.24)

Сумма средних значение Рср всех вертикальных переменных сил определяется по формуле:

Скачать файл