Расчеты верхнего строения пути. Расчеты пути на прочность. Классификация рельсов по длине. Расчеты бесстыкового пути, страница 26

Вероятностью отказа называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени возникнет хотя бы один отказ. Отказ и безотказная работа являются событиями несовместимыми и противоположными, поэтому

,                                                

,                                              ()

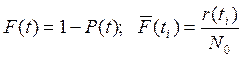где r(t_i) – число отказов к моменту времени t_i.

Плотностью распределения наработки до отказа называется отношение числа отказавших объектов в единицу времени к первоначальному числу испытываемых объектов при условии, что все вышедшие из строя объекты не восстанавливаются.

Плотность распределения наработки до отказа f(i) является дифференциальной формой закона распределения наработки до отказа:

;

                                        ()

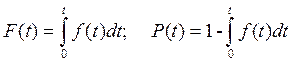Плотность f(t) является неотрицательной функцией, причем

.

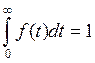График f(t) часто называют кривой распределения наработки до отказа.

Статистическая оценка плотности вероятности безотказной работы имеет вид

,                                               ()

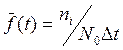где n_i – число отказавших деталей в интервале времени Δt/

Интенсивностью отказов называется отношение числа отказавших объектов в единицу наработки к числу объектов, безотказно работающих к рассматриваемому моменту времени:

.                                             ()

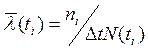Вероятностная оценка интенсивности отказов находится из выражения

.                                                ()

Интенсивность отказов представляет собой условную плотность вероятностей возникновения отказа невосстанавливаемого объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказа не произошло.

Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью

.                                                  ()

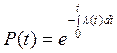Важнейшей из характеристик является средняя наработка до первого отказа, которая определяется как математическое ожидание величины t:

.                     ()

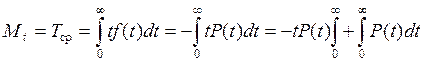Так как t положительно и P(0)=1, а P(∞)=0, то

.                                                 ()

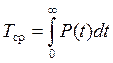По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле

,                                              ()

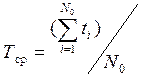где t_i – время (наработка) безотказной работы i-го образца изделия;

N₀ – число испытуемых образцов.

Основной характеристикой рассеивания случайной величины является дисперсия этой величины, которая определяется как

.                                            ()

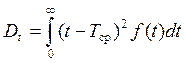Статистическая оценка дисперсии величины t имеет следующий вид:

.                                      ()

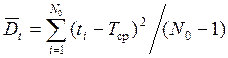За меру рассеивания принимают также среднее квадратическое отклонение (или стандарт), равное квадратному корню из дисперсии, взятому с положительным знаком

.                                                   ()

Если нужно оценить степень рассеивания ряда t_i при помощи безразмерной характеристики, то в этом случае используют коэффициент вариации, определяемый как

.                                                           ()

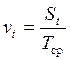Рассмотренные критерии надежности позволяют достаточно полно оценить надежность невосстанавливаемых изделий. Они также позволяют оценить надежность восстанавливаемых изделий до первого отказа.

5.8.2 Модели эксплуатационных отказов элементов верхнего строения пути

Исчерпывающей характеристикой надежности устройств с непрерывным характером работы служит закон распределения времени безотказной работы. Если известен вид закона и его параметры, то легко определить любую, интересующую нас, характеристику надежности.

В качестве теоретических распределений наработки до отказа могут быть использованы любые, применяемые в теории вероятностей, непрерывные распределения. Наиболее распространенными законами распределения отказов являются экспоненциальный и нормальный.

Экспоненциальное распределение характерно для внезапных отказов элементов и систем. Плотность вероятности экспоненциального распределения случайной величины задается уравнением

,                                             ()

где λ — интенсивность отказов — величина, обратная наработке до отказа λ=1/Т_ср;

е — основание натуральных логарифмов.

Если отказы исследуемых объектов подчиняются экспоненциальному закону, то для данного объекта в данных условиях эксплуатации λ=const, т. е. в равные промежутки наработки число отказавших объектов, приходящихся на каждый оставшийся работоспособным к этому моменту наработки, будет постоянным.

Другие характеристики экспоненциального распределения: средняя наработка до первого отказа Т_ср=1/λ;дисперсия D_t=Т_ср;вероятность безотказной работы

.                                                ()

Нормальный закон распределения (закон Гаусса) часто хорошо согласуется с экспериментальными данными при испытаниях на надежность. Это относится прежде всего к таким процессам, при которых отказы вызываются многими равновлияюшими причинами. Параметрами распределения для нормального закона являются Т_ср и σ_t. Плотность распределения случайной величины задается уравнением

.                                             ()

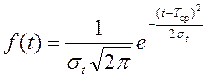Расчеты удобно производить, если указанное выражение привести к более простому виду. Для этого начало координат надо переместить на ось симметрии, т. е. в точку Т_ср и наработку представить в относительных единицах, а именно в частях, пропорциональных среднему квадратическому отклонению. При этом необходимо заменить переменную величину другой

,                                                        ()

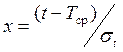а величину среднего квадратического отклонения принять σ_t=1. Тогда в новых координатах получим так называемую центрированную и нормированную функцию, плотность распределения которой

.                                                      ()

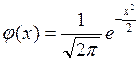Значения этой функции приведены во многих математических справочниках. Площадь под кривой φ(х) в пределах -∞<x<∞ равна 1.

Интегральная функция

,                                  ()

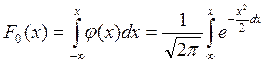которая является функцией нормального распределения, также протабулирована и ею удобно пользоваться при расчетах.