Коэффициент относительной жесткости рельсового основания и рельса К - одна из важнейших характеристик для расчета пути на прочность, изменяющаяся в пределах от 0,009 до 0,018 для типовых конструкций пути.
2.3 Определение нагрузок
Рельс испытывает нагрузку от колес подвижного состава. Между колесами на него действует только реакция основания (отпор) q. Вывод основных формул расчета балки на сплошном упругом основании под одной сосредоточенной нагрузкой Р дается в «Сопротивлении материалов».
Исходя из теоремы Шведлера-Журавского для изогнутой оси рельса (как балки, лежащей на сплошном упругом основании), между точками опирания колес будем иметь, что:
- изгибающий момент в балке равен второй производной функции ординат изогнутой оси балки по ее длине, умноженной на жесткость балки, т. е. на произведение модуля упругости материала балки Е на момент инерции ее сечения:
.
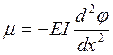(4)
Поперечная сила Qп равна третьей производной (от той же функции), умноженной на жесткость балки:
.
(5)
Реактивный отпор, т. е. величина реакции упругого основания, действующий на одну погонную единицу длины балки qx, равен четвертой производной, умноженной на жесткость балки:
. (6)
Подставляя в уравнение (6)
вместо qx его значение, по формуле (З) получим, что
Отсюда и получается основное линейное дифференциальное уравнение для расчета
.
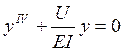Для решения этого дифференциального уравнения с постоянными коэффициентами (для заданного пути величины U и EI постоянные) составляют характеристическое уравнение, при этом вводят следующее обозначение:
,
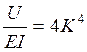(7)
Тогда дифференциальное уравнение примет вид:
.
Из равенства (7) получаем, что
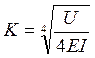, см-1.
(8)
Величина U характеризует жесткость рельсового основания, а EI - жесткость рельса. Поэтому коэффициент K называют коэффициентом относительной жесткости рельсового основания и рельса.
Интегрируя указанное дифференциальное уравнение и используя известные граничные условия (при х=∞ у=0, при х=0 у'=0, при х=0 Q=P/2) получим следующие основные ???, которыми и пользуются при расчетах пути.
Изгибающий момент
,
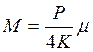(9)
Упругий прогиб в любой точке
.
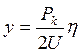(10)
При расчетах пути на прочность требуется также определять давление на шпалу. Очевидно, что если интенсивность реактивного отпора на единицу длины рельса равна q, а расстояние между осями шпал равно 1, то на одну шпалу придется давление, равное Q, где
.
(11)
Подставляя в формулу (11) выражение q из формулы (3), а затем выражение у из формулы (10), получим зависимость для определения давления на шпалы
.
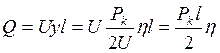(12)
Следовательно, М пропорционален µ, а у и Q – ординатам линии влияния η.
Анализируя последние 3 формулы, замечаем,
что изгибающий момент, упругий прогиб и давление на шпалу равны постоянным для
заданных условий величинам (соответственно 
,
и 
),
умноженным на µ или η.
Следовательно, изгибающий момент прямо пропорционален µ, а упругий прогиб и давление на шпалу прямо пропорционален η.
Величины µ и η получаются в процессе интегрирования дифференциального уравнения и представляют собой следующие функции от переменных kx:
,
(13)
.
(14)
Задаваясь различными значениями х и зная k, можно вычислить ординаты µ и η для любого сечения х и вычертить их эпюры. Для этого можно воспользоваться таблицами значений µ и η.
2.4 Построение эпюр µ и η
Определим характерные точки эпюры µ.
При х=0 величина kx=0; cos kx=l, sin kx=0. Тогда из уравнения (13) получим, что при х=0, т.е. в начале координат, µ=1 (величина отвлеченная).
Из того же уравнения видно, что µ=0 при kx=π/4, а также при величинах kx на π, 2π, Зπ и т. д. больших, чем π /4. Следовательно, первая нулевая точка будет при kx=π/4, т. е. когда х=π/(4k), вторая - при х=5π/(4k); третья - при x=9π/(4k) и т. д. Следовательно, эпюра µ для случая приложения силы Р в сечении O будет иметь следующий вид:
Подсчёт отрицательного момента показывает, что его наибольшая величина (при µ=-0,208) от наибольшего значения момента (под грузом) составляет 21%, причём это соотношение между наибольшими положительными и отрицательными моментами не зависит от конструкции пути. Другой особенностью эпюры является быстрое затухание последовательных волн. Силы, которые приложены от данного сечения на расстоянии 3,5 м и далее, оказывают на рельс ничтожно малое влияние, которым можно пренебречь. Поэтому обычно ограничиваются положительной средней частью эпюры и только двумя симметрично примыкающими к ней отрицательными полуволнами.
Из формулы (13) получается,
что в сечении, соответствующем х=0, где приложена сила P1., величина µ=1. Следовательно, изгибающий момент в этой
точке будет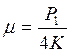 
, а далее, в обе стороны от точки О µ
будет убывать, и в соответствии с формулой (9) будет уменьшаться величина
изгибающего момента от силы P1.
В каком-нибудь сечении, отстоящем от точки О на расстоянии х=а, т.е. в точке О1 величина µ равна µа и, следовательно, изгибающий момент в этой точке О1 от силы P1, приложенной в точке 0, будет равен
.
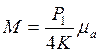Представим, что мы имеем другую силу Р1, приложенную в точке О1 (пунктир на рисунке), и хотим определить, какую надо взять величину µ, чтобы подсчитать изгибающий момент от этой силы Р1 в сечении 0.
Рисунок
Очевидно, это будет та же величина µа, т. к. сечение балки и упругая характеристика её основания на всём протяжении одинаковы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.