Для «стареющих» элементов в качестве распределения интервала безотказной работы используют обычно нормальное распределение. Для определения параметров нормального распределения Tср и σt можно применить метод квантилей в сочетании со способом наименьших квадратов.
Частота отказов элементов рельсовых скреплений типов КБ-65, БП-65, ЖБР-65 определяется на основании статистических данных об отказах элементов во время эксплуатации. После определения параметров Tср и σt, и вероятности безотказной работы Pj(t) отдельных элементов скреплений переходят к определению вероятности безотказной работы узлов скреплений. Для этой цели составляются схемы анализа надежности скреплений КБ, ЖБР и БП.
При составлении структурных схем исходным было положение, что система последовательно соединенных элементов работоспособна тогда и только тогда, когда работоспособны все ее элементы. Вероятность безотказной работы системы из последовательно соединенных элементов определим по формуле ().
При параллельном соединении отказ системы происходит тогда и только тогда, когда откажут все параллельные участки схемы. Вероятность безотказной работы участков схемы, состоящей из параллельных цепей, определим по формуле ().
При составлении структурных схем для подкладочных скреплений КБ и БП учитывалось то, что подкладки объединяют работу прикрепителей (клеммных и закладных болтов). Отказ узла скреплений в экстремальных условиях эксплуатации произойдет тогда, когда откажут обе параллельные цепи элементов прикрепителей. У бесподкладочных скреплений ЖБР отказ узла скреплений наступит при отказе любого из его элементов.
Вероятность безотказной работы узлов рельсовых скреплений определяем по формулам:
для узлов скреплений типа КБ
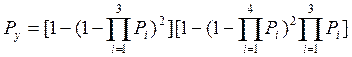 ;
()
;
()
для узлов скрепления типа БП
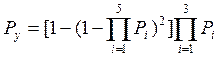 , ()
, ()
для узлов скрепления типа ЖБР
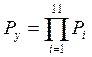 .
()
.
()
Однако отказ узла скрепления еще не означает отказа всей системы связей рельса с основанием. Согласно нормативным документам поперечная устойчивость рельсовых нитей и всей рельсошпальной решетки обеспечивается, если нет кустов из трех негодных шпал, а рельсовая нить не расшита более чем на трех или шести шпалах подряд. Справедливость этих требований подтверждается результатами проведенных в последнее время исследований поперечной устойчивости пути на железобетонных шпалах под поездной нагрузкой.
В соответствии с этими требованиями рассмотрим систему, состоящую из последовательно соединенных элементов, каждый из которых имеет по два резервных нагруженных элемента. Предположим, что все элементы системы однотипны, тогда вероятность безотказной работы системы поперечных связей составит
![]() .
()
.
()
Значения вероятности безотказной работы поперечных связей рельсов с основанием, определенные по формулам () для пути с железобетонными шпалами и скреплениями типов КБ, БП, ЖБР приведены на рис. 4.46. Из анализа этих данных следует, что наибольшей вероятностью безотказной работы обладают скрепления типа КБ, а наименьшей — скрепления типа ЖБР. Из рисунка видно, что если по участкам пути со скреплениями типа КБ можно пропустить до 350 млн. т брутто груза без существенного обновления элементов скреплений, то по пути со скреплениями ЖБР — не более 200 млн. т брутто.
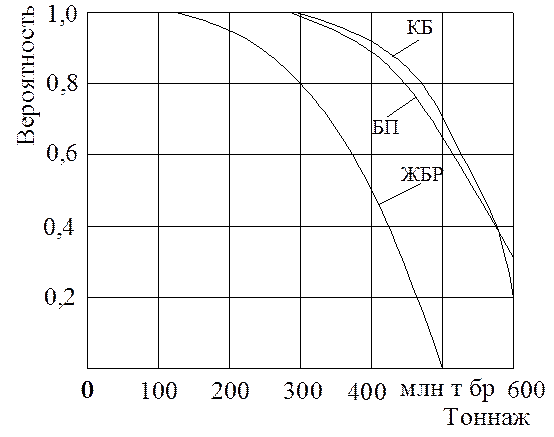
Рисунок – Кривые вероятности безотказной работы скреплений КБ, БП, ЖБР
5.9 Определение продольной деформации рельсовых плетей
Величина продольной деформации зависит от погонного и стыкового сопротивления. При укладке уравнительных рельсов необходимо учитывать следующие обстоятельства:
1. Между стыкуемыми плетьми необходимо иметь хотя бы 1 уравнительный рельс. Это обеспечивает возможность разрядки напряжений при производстве работ;
2. Чем больше стыковое сопротивление, тем сложнее устройство стыка и изолирующего в особенности.
Исходя из вышеизложенного будем принимать, что стыкование рельсовых плетей одна с другой производится при помощи 2-3 рельсов длиной 12,5 м. Основное условие укладки уравнительного рельса заключается в следующем: суммарная температурная деформация уравнительного рельса и концевого участка плети не должна превышать 21 мм.
В общем случае температурная деформация рельсовой плети определяется по формуле
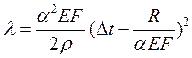 ,
,
|
где α |
- |
коэффициент линейного расширения рельсовой стали; |
|
Е |
- |
модуль упругости рельсовой стали; |
|
F |
- |
площадь поперечного сечения рельса; |
|
∆t |
- |
перепад температур от момента закрепления плети до достижения минимальной и максимальной температуры. |
Удлинение плети от момента закрепления максимальной до наступления температуры
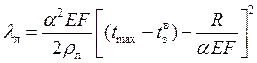 .
.
Сокращение длины плети от момента укладки до наступления минимальной температуры
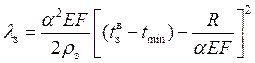 .
.
Суммарное перемещение плети
![]() .
.
Суммарное годовое перемещение уравнительного рельса определяется по формуле
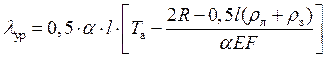 ,
,
|
где l |
- |
длина уравнительного рельса; |
|
Та |
- |
годовая амплитуда изменения температуры. |
Пример расчета продольной деформации рельсовой плети
и уравнительных рельсов
Исходные данные:
|
tmax=+57 °C; |
E=2,1∙106 кг/см2; |
|
tmin=-48 °C; |
α=0,0000118; |
|
ρл=6,5 кгс/см; |
|
|
ρз=25 кгс/см; |
R=20000 кг. |
Удлинение плети от момента наступления максимальной температуры до момента закрепления
![]()
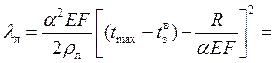
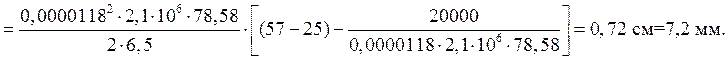
Сокращение длины плети от наступления минимальной температуры до момента закрепления плети
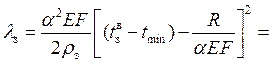
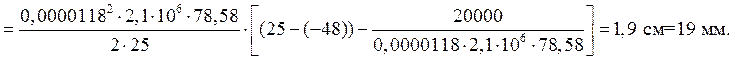
Суммарное годовое перемещение уравнительного рельса
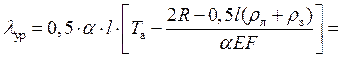
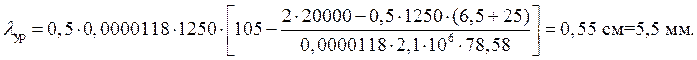
Суммарное годовое перемещение плети
![]()
Суммарное перемещение трех рельсов уравнительного пролета
![]()
Суммарное перемещение плети и уравнительных рельсов
![]()
Суммарная величина конструктивных зазоров между тремя уравнительными рельсами
![]()
Сравнивая суммарное перемещение плети и уравнительных рельсов с суммарной величиной конструктивных зазоров можно сделать вывод, что разность 1,4 мм летом может привести к появлению незначительного торцевого давления, а зимой к изгибу болтов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.