Значения функции F0(x), приведенные в таблицах, даются обычно при х≥0. Если х оказывается отрицательным, надо воспользоваться формулами
![]() ;
; ![]() . ()
. ()
Обратный переход от центрированной и нормированной функции к исходной делается по формулам:
![]() ; ()
; ()
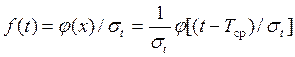 . ()
. ()
Иногда пользуются нормированной функцией Ф0(х) с другими пределами интегрирования, определяемой выражением
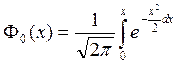 ()
()
и называемой нормированной функцией Лапласа. Очевидно, что для х≥0
![]() .
.
При этом следует учитывать, что Ф0(х) функция нечетная, т. е.
![]() .
()
.
()
Эксплуатировать конструкции пути до полного отказа всех элементов невозможно, поэтому для определения параметров распределения используют усеченные выборки.
В случае усеченной выборки, когда в результате испытаний объектов получены R возрастающих значений наработки (R<N0) для отказавших объектов t1, t2, …, tr, а N0-r объектов по истечении некоторого времени t0>tr остались исправными, параметры Тсри σt можно оценить по методу квантилей следующим образом.
Считаем, что за время ti вероятность выхода из строя испытываемых объектов составляет
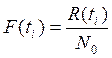 .
()
.
()
Для этой вероятности определяем квантили Uр и составляем R уравнений:
![]()
![]() ;
;
![]() ;
;
………………... ()
![]()
Полученную систему уравнений решаем по методу наименьших квадратов, для чего умножим левые части каждого из уравнений системы на Up1, Up2, ...,Upr соответственно и все R уравнений сложим, в результате получим первое, так называемое, нормальное уравнение
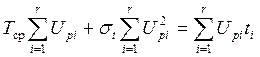 .
()
.
()
Второе нормальное уравнение получим суммированием уравнений системы ():
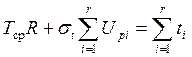 . ()
. ()
Уравнения () и () решаем относительно неизвестных Тср и σt, и находим, таким образом, их оценки.
5.8.3 Оценка и прогнозирование надежности рельсов и скреплений
Для оценки надежности рельсов необходимы сведения об их отказах с момента укладки в путь. Такие данные можно взять из ведомостей учета рельсов, снятых с главных путей по изломам, порокам и повреждениям (ПУ-4) и рельсо-шпалобалластных карт.
Данные об отказах рельсов, включаемых в одну совокупность, должны отвечать набору определяющих признаков: по типу рельсов (с учетом термообработки), роду шпал, балласта, плана и профиля пути, а также грузонапряженности, осевым нагрузкам, скоростям движения. Длина анализируемого участка пути определяется необходимой точностью получения показателей надежности рельсов. При планировании статистического эксперимента необходимо предусматривать объем выборки не менее 800 рельсов, т. е. длина анализируемого участка с однотипным верхним строением пути должна быть не менее 10 км. Из многочисленных наблюдений известно, что с ростом пропущенного тоннажа интенсивность отказов рельсов увеличивается.
В теории надежности для систем с возрастающей интенсивностью отказов наиболее часто используется нормальное распределение. Плотность распределения отказов рельсов задается уравнением (), а интегральная функция распределения — уравнением ().
Нормальное распределение является двухпараметрическим: заданием параметров Тср и σt, полностью определяется распределение.
Данные об отказах рельсов на некотором участке пути представляют собой вариационный ряд случайных чисел наработки до отказа (таблица ).
Таблица – Параметры отказов рельсов
|
Наработка ti, млн. т. |
Частота R(ti), шт./км |
Частость |
Квантиль Upi |
|
266 |
0,52 |
0,00650 |
2,49 |
|
429 |
0,98 |
0,01225 |
2,25 |
|
591 |
1,58 |
0,01975 |
2,06 |
|
751 |
2,10 |
0,02625 |
1,94 |
|
902 |
3,60 |
0,04500 |
1,70 |
|
1064 |
5,60 |
0,07000 |
1,48 |
Квантили Upi определяются по значениям частости F(ti) с использованием специальных таблиц. Используя данные табл. !!!, запишем для каждой наработки ti уравнения ():
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Складывая левые и правые части уравнений, получим
![]() .
.
Умножая левые и правые части уравнений на квантили Upi и аналогично складывая, найдем
![]() /
/
Значения параметров Tср и σt, получим решая систему полученных двух уравнений. Для
рассматриваемого случая Tср=2300 млн. т, σt=822 млн. т. Имея параметры Tср и σt, можно для любой наработки ti определить вероятность отказа ![]() , а также количество отказавших рельсов на
километр пути к времени наработки ti
, а также количество отказавших рельсов на
километр пути к времени наработки ti
![]() ,
,
где 80 — число рельсов длиной 25 м на одном километре пути.
Конструкция верхнего строения пути является сложной системой, состоящей из многих элементов. При расчете показателей надежности рельсовых скреплений различных типов приходится рассматривать структурные схемы, включающие последовательное и параллельное соединения элементов.
Скрепления проектируют так, что обычно у него нет функционально «лишних» деталей. Отказ любой из них сильно снижает эффективность функционирования узла скрепления, вызывает интенсивный износ соседних деталей и повышает расходы на содержание пути. Поэтому, оценивая надежность скреплений различных типов в условиях нормальной эксплуатации, все элементы необходимо считать соединенными последовательно, а вероятность безотказной работы узла такой системы оценивать по формуле
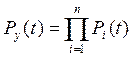 ,
()
,
()
где Pi(t) — вероятность безотказной работы i-го элемента.
Оценивая надежность скрепления в экстремальной ситуации, в которой конструкция может находиться ограниченное время, после чего переходит в аварийное состояние, отдельные цепи элементов можно считать параллельными. Безотказность работы элементов цепи
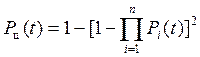 .
()
.
()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.