Расчеты верхнего строения пути. Расчеты пути на прочность. Классификация рельсов по длине. Расчеты бесстыкового пути, страница 8

Отсюда, в соответствии с законом независимости действия сил вытекает правило определения изгибающего момента в каком-либо сечении О балки на упругом основании при действии не одной, а нескольких сил: для этого надо, пользуясь эпюрой µ, построенной для сечения О, величину каждой силы умножить на значение µ, соответствующее точке приложения этой силы, и сумму этих произведений разделить на 4k. Величины µ необходимо брать с соответствующим знаком.

Положим, на балку действуют три силы: Р₁, Р₂ и Р₃. Величина изгибающего момента от действия этих сил в точке О составит:

,

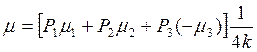а в общем виде

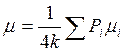.                                                     (15)

Рисунок

Из рисунка отмечаем, что:

1)  При действии двух-трех сил М может оказаться меньше М от действия одной силы.

2)  На величину М существенное влияние оказывают расстояния между силами.

2.5 Выбор расчётной оси

При определении воздействия на путь заданной системы нагрузок приходится выяснять, под какой именно осью в данном сечении будет возникать наибольший изгибающий момент, т.е. какая ось является расчётной.

Рисунок

Для этого в расчётном сечении ставят сначала первую ось экипажа и определяют М, затем сдвигают всю систему грузов так, чтобы вторая ось стала над расчётным сечением, и снова определяют М, и т.д., чтобы рассмотреть все возможные положения, при которых более тяжёлые оси стоят над большими положительными ординатами эпюры µ.

Сравнивая затем итоги, определяют, при каком положении системы грузов получается наибольший изгибающий момент. Ось, которая при этом окажется над расчётным сечением, и будет расчётной осью.

Аналогично устанавливаются зависимости, определяющие величину давления на шпалу и величину упругого прогиба рельсов от статического приложения системы грузов.

Из уравнения (14) видно, что при х=0 получим η=1. Поэтому при х=0 и при Р=1 максимальное давление на шпалу составляет

.

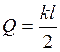Из уравнений (10) и (12) видно, что давление на шпалу и прогиб у будут равны нулю везде, где η=0, а это будет тогда, когда sin kx и cos kx будут равны по величине, но противоположны по знаку. Это имеет место при kx=3π/4 и далее через π.

Следовательно, первая нулевая точка, будет при x=3π/(4k), вторая при х=7π/(4k) и т.д.

Эпюра η будет иметь вид, показанный на рис. Необходимо иметь ввиду то, что нулевая точка на эпюре µ (и эпюре М) в три раза ближе к сечению О, чем на эпюре η (и эпюрах давления на шпалу и прогиба). Максимальное отрицательное значение η=-0,0432, т.е. всего 4% от значения η. Следовательно, величина прогиба рельса, вверх составляет максимум 4% величины прогиба вниз в сечении под грузом.

Аналогично порядку определения М от нескольких сил, исходя из эпюры η и применяя уже известные обозначения, получим расчетные формулы для Q и у от системы грузов

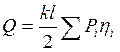,                                                 (16)

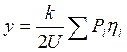,                                                (17)

где Q	–	давление рельса на шпалу;
Pi	–	вертикальная сила, действующая на рельс;
U	–	модуль упругости рельсового основания;
L	–	расстояние между осями шпал;
ηi	–	ордината под точкой приложения силы Pi эпюры η, построенной для сечения О;
k	–	коэффициент относительной жесткости рельсового основания и рельса, см-1.

Определение напряжений

Напряжение от статического воздействия системы грузов в рельсах определяется делением М от системы грузов в сечении под этой осью на момент сопротивления сечения рельса

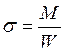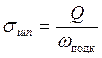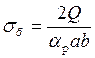;     ;     .   Проверить формулы!!!!

3 Практический способ расчета пути на прочность

3.1 Предпосылки и допущения расчета

Под воздействием подвижного состава в элементах ВСП возникают напряжения и деформации. Зависимость их от сил, действующих на путь, как и колебаний подвижного состава, сложна и пока не поддается точному определению. Поэтому в Правилах расчета железнодорожного пути на прочность приняты следующие предпосылки и допущения:

1)  расчет ведется по формулам статического расчета; переменные динамические силы от расчетного колеса принимаются в их максимальном вероятном значении, от остальных колес – в их среднем значении;

2)  рельс рассчитывается по напряжениям изгиба; контактные, напряжения под головкой и другие линейные напряжения не учитываются. Предполагается, что уровень изгибных напряжений характеризует в известной степени и местные напряжения в рельсах;

3)  характеристики пути (модуль упругости и др.) принимаются детерминированными;

4)  рельс рассматривается как неразрезная балка, лежащая на сплошном упругом основании (рассматривается сечение, удаленное от стыка на 3,5 м и далее);

5)  упругая реакция основания q считается линейно зависящей от осадки y, т.е. q=-Uy, где U - коэффициент пропорциональности, или модуль упругости подрельсового основания;

6)  расчет ведется на вертикальные силы, приложенные по оси симметрии рельса. Учет действия горизонтальных поперечных сил, влияние внецентренного приложения вертикальных сил и подуклонки рельсов осуществляется умножением расчетных напряжений в подошве рельса на коэффициент f; из продольных сил учитывается только температурные силы, появляющиеся в рельсах;

7)  колеса подвижного состава при движении не отрываются от поверхности катания рельсов (рассматривается безударное движение);

8)  при действии на путь системы грузов используется закон независимости – напряжения и деформации в рассматриваемом сечении складываются с учетом их величины и знака;

9)  путь и подвижной состав находятся в исправном состоянии, отвечающим требованиям ПТЭ;

10)  за критерий  прочности рельсов принимаются допускаемые напряжения, а не долговечность и не ресурс;