По исследованиям С.П.Тимошенко наибольший дополнительный прогиб рельса от проходящих по нему с неровностями колес зависит от соотношения То/Тψ ,
где То – время, в течение которого колесо проходит расстояние, равное длине неровности;
Тψ – период собственных колебаний системы “колесо-рельс”.
Дополнительный прогиб рельса определяет собой дополнительное вертикальное усилие. На основании теории колебаний Тимошенко доказал, что
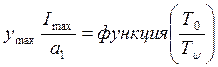
Указанная зависимость представлена в виде графика, который уточнил К.П.Королев. При глубине неровности 1см график имеет вид:
Дополнительное вертикальное усилие на рельс от воздействия ИНК равняется
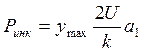
где а1 – глубина неровности, 1см.
Период собственных колебаний системы “колесо-рельс”
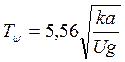
где g – ускорение силы тяжести (9,81 см/с2).
При этом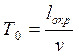 
; подставив l см,
а v км/ч, получим
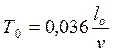
Из графика видно, что ymax=1,47
в том случае, когда при данной длине синусоидальной неровности скорость
приобретает такое значение, что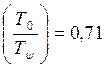 
(с увеличением v это
соотношение достигается при больших скоростях движения).
По формулам () определяем
Тφ и время прохождения колесом неровности длиной соответственно 20 см и πd (
и 
).
Если получается неравенство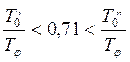 
,
то очевидно ymax надо принимать равным 1,47 (как наибольшая величина в
интервале значений).
Если для обоих крайних случаев неровности То/Тφ больше или меньше 0,71, ymax находят по графику, при этом из двух величин берут наибольшую.
На основании исследований закономерностей изменения динамических давлений установлено, что среднее значение этих инерционных давлений равно 0, а наибольшее равно 4Sинк, т.е.
(Ринк)max=0+4Sинк, отсюда
Sинк=0,25(Ринк)max=0,25ymax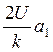 
.
()
Количество колес, имеющих изолированные неровности на поверхности катания практически невелико, поэтому Sинк вводится в расчет величиной 0,05.
После перехода к системе СИ формула для Sинк примет вид
,
|
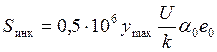где α |
- |
коэффициент учета взаимодействия массы пути и необресоренной массы экипажа (деревянные шпалы – 0,433, а железобетонные – 0,403); |
|
e0 |
- |
расчетная глубина изолированной неровности, принимаемая 2/3 от наибольшей глубины ползуна на колесах по ПТЭ (для локомотивов с подшипниками скольжения e0=0,067·10-2 м и качения e0=0,047·10-2, а вагонов соответственно e0=0,133·10-2 м и e0=0,067·10-2 м); |
|
ymax |
- |
максимальный дополнительный прогиб рельса, отнесенный к единице глубины неровности (безразмерная величина). |
3.2.5 Определение Рннк и Sннк
Наиболее распространенными являются так называемые непрерывные неровности на колесе, когда из-за неравномерности износа искажается первоначальная форма колеса по всей поверхности катания.
Для учета этих сил принята эмпирическая формула, т.к. сложно принять форму непрерывной неровности на колесе. Непрерывные неровности на колесах являются обычно следствием неравномерного износа поверхности катания (износ носит незакономерные, случайный характер).
.
()
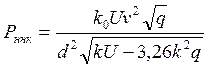Исследования закономерностей изменения инерционной силы, вызванной ННК, показывают, что среднее значение этой силы равно нулю, а максимальное – 4,5Sннк, т.е.
(Рннк)max=0+4,5Sинк, отсюда
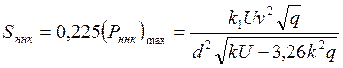
где к1=0,225к0.
Для вагонных и локомотивных колес к1=0,052; к0=к1/0,225.
Величина Sннк вводится в формулу () коэффициентом 0,95.
После перехода к системе СИ формула для Sннк примет вид
,
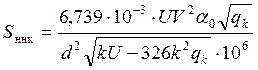где d – диаметр колеса.
3.3 Определение напряжений
По формуле (1.21) определяется среднеквадратическое всех сил, а по формулам (1.22), (1.23) – эквивалентные силы.
Напряжения в кромке подошвы рельсов от изгиба определяются по формуле:
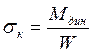
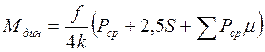
Динамические средние напряжения смятия шпалы подкладкой определяется по формуле:
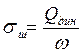
где ω – площадь подкладки в см2.
Наибольшие динамические напряжения в балластном слое возникают под шпалой на уровне ее нижней постели в подрельсовом сечении. Средняя их величина определяется по формуле:
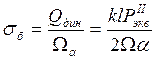
где Ωα-αab/2, т.е. опорная площадь полушпалы с учетом коэффициента α изгиба шпалы.
Основной составляющей S является Sнп. Поэтому когда не требуется большая точность, а также при предварительных расчетах эквивалентные силы можно определять по приближенным эмпирическим формулам:
,
РИС
Напряжения на основной площадке земляного полотна
где 
- напряжение на
основной площадке, вызванное давлением
расчетной шпалы;
и 
- напряжения, обусловленные давлением смежных шпал с
обеих сторон.
3.4 Определение расчетного положения нагрузки
Для определения напряжений в элементах пути приходится решать вопрос о том, под какой же осью эти напряжения или прогиб будут наибольшими. Эта ось и будет расчетной в любом сечении пути. При определении напряжений от изгиба в рельсах за расчетную ось принимают крайнюю ось двухосной и трехосной тележки. При определении напряжений в шпалах, балласте и основной площадке земляного полотна за расчетную ось при двухосной тележке принимают крайнюю, а при трехосной тележке при положительных значениях ординаты η для соседних осей за расчетную ось надо принимать среднюю, а при отрицательных значениях – крайнюю ось.
Определение расчетного экипажа
По рассматриваемому участку движутся грузовые и пассажирские локомотивы, четырех-, шести- и восьмиосные вагоны с обычными и повышенными осевыми нагрузками, а также дизель- или электропоезда и пассажирские вагоны.
Для приближенных расчетов при определении напряжений в
рельсах для всех видов обращающегося подвижного состава 
может
быть определена по формуле:
.
Расчет напряжений в рельсах и определение расчетного экипажа для заданных условий эксплуатации целесообразнее выполнять в табличной форме:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.