Расчеты верхнего строения пути. Расчеты пути на прочность. Классификация рельсов по длине. Расчеты бесстыкового пути, страница 6

2 Расчеты пути на прочность

2.1 Основные положения статического расчета

В основе статического расчета пути на прочность лежит гипотеза Фукса-Винклера, которая предполагает, что между силой и деформацией существует линейная зависимость

,                                                              (1)

где р - реактивное давление упругого основания, кгс, на 1см² постели шпалы;

у - упругая просадка шпалы, см;

с - коэффициент податливости основания (коэффициент постели шпалы), кгс/см².

В дальнейшем Васютинский определил численные значения с и довел теорию до практического применения (с=1÷60, с_ср=6), а Петров применил ее для динамического расчета.

Обычно рельс рассматривается как балка бесконечной длины, неизменного сечения, лежащая на сплошном упругом однородном основании с двухсторонними реакциями. При современных конструкциях пути разница в расчетах по сравнению с балкой на многих упругих точечных опорах не превышает 5-7%.

Двухсторонними упругими реакциями основания реальный путь не обладает, т. к. ни балласт, ни грунт на растяжение не работают; сопротивляется выгибу рельса вверх лишь его вес и вес опор, если рельс к ним плотно прикреплен.

Основной характеристикой для статического расчета является связь между упругим прогибом у в каждом сечении и погонным упругим отпором q в том же сечении. При нелинейной зависимости эта связь выражается в виде .

Знак минус поставлен потому, что направление упругого отпора q всегда обратно упругому прогибу, его вызвавшему.При линейной зависимости , т.е. без учета знака .

Обычно параметр U определяется экспериментально.

2.2 Расчетные характеристики пути

Для характеристики упругих свойств основания рельса по его длине пользуются модулем упругости U, кгс/см², который численно равен распределенному реактивному отпору основания, возникающему на единице длины рельса при упругой осадке, равной единице.

Схема передачи сил на шпалы

Упругие линии прогибов под нагрузкой

Формулы

где D - расчетная характеристика полушпалы, численно равная силе, вызывающей упругую просадку ее в подрельсовом сечении, равную единице длины;

1 - расстояние между осями шпал (при эпюре 1600 шт/км 1=63 см; при 1840 и 2000 шт/км соответственно 55 и 50 см);

а и b - соответственно длина и ширина шпалы, см;

α- коэффициент изгиба шпалы - отношение средней просадки у_ср. к просадке в подрельсовом сечении у_р (у деревянных шпал у_mах располагается в подрельсовом сечении, у ж.б. шпал оно несколько сдвинуто к торцам шпал). Для деревянных шпал и щебеночного балласта летом α=0,70-0,85; зимой - в полтора раза меньше;

с - коэффициент постели, численно равный силе, приложенной к единице площади основания и вызывающей просадку, равную единице длины (для участка пути с деревянными шпалами и щебеночным балластом с изменяется отзимой – до и более; для ж. б. шпал с будет выше). Размерность с - кгс/см²/см.

Модуль упругости подрельсового основания зависит от материала, размеров и состояния прокладок, шпал, балласта, земляного полотна, подстилающего слоя грунта, температурного состояния полотна (замерзшее или талое), от эпюры шпал и т. д. От типа рельсов U не зависит.

Реакция (отпор) сплошного упругого основания q_x. равна интенсивности погонного давления рельса на основание. Следовательно, при упругой просадке рельсовой нити в 1см a при любой другой просадке -  (3).

Величина модуля упругости рельсового основания при деревянных шпалах летом для разных конструкций пути составляет 200-300 кгс/см², а в зимнее - 450-500 кгс/см². При железобетонных шпалах путь более жесткий, чем при деревянных. На основании исследований ЦНИИ МПС и МИИТа модуль упругости рельсового основания стабилизированного пути с ж. б. шпалами может приниматься равным 1700-2000 кгс/см². Однако при прочностных расчетах такого пути следует делать еще и дополнительный проверочный расчет на первый период после укладки (или после капитального ремонта пути), т.е. для нестабилизированного пути, когда модуль упругости составляет около 500 кгс/см².

Модуль упругости пути, как и жесткость, является случайной, переменной в пространстве и времени, величиной.

Расчетные значения U на щебеночном балласте:

Шпалы и эпюра шпал	U, кгс/см2
	летом	зимой
Ж.б. 1840 шт/км 2000	680 720	1200 1300
Деревянные 1840  2000	230 300	400 500

При асбестовом балласте модуль упругости уменьшается на 10-20%.

Специальными исследованиями установлено оптимальное значение U в круглогодичном цикле от 500 до 1000 кгс/см². Излишняя жесткость пути увеличивает динамическое взаимодействие пути и подвижного состава. Укладкой в путь упругих элементов можно достигнуть требуемого значения модуля.

Для получения оптимального модуля упругости подрельсового основания его следует проектировать, т.е., имея ввиду, что подрельсовое основание является многослойным, задавать нужные свойства каждому слою. Влияние каждого слоя (подрельсовые прокладки, путевые подкладки, нашпальные прокладки, подрельсовое основание, балласт, земляное полотно) на модуль упругости можно определить. Общий упругий прогиб всех слоев

,

где y_i - линейная упругая деформация каждого слоя, находящегося под воздействием упругого отпора q.

.

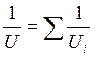Жесткость пути численно равна силе давления колеса на рельс Р, отнесенной к упругому прогибу у под силой

;   ;   ;   ,

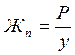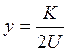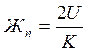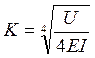где К - коэффициент относительной жесткости рельсового основания и рельса, см^-1;

I - момент инерции поперечного сечения рельса относительно его центральной горизонтальной оси, проходящей через центр тяжести сечения, см⁴.

Пример. Рельсы Р65 (с износом 6 мм) I=3208 см⁴, балласт щебеночный. На деревянных шпалах при U=270 кгс/см²

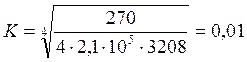 см; 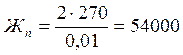   кгс/см.

На ж. б. шпалах при U=1000 кгс/см²

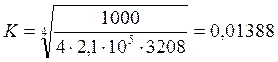 см; 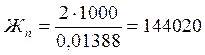   кгс/см.

Зимой при увеличении U до 500 кг/см² и 2000 кгс/см² жесткость пути будет соответственно равна 100000 и 288040 кгс/см. Жесткость пути определяется под статической нагрузкой, эту же Ж_п. принимают и при динамических расчетах.