Расчеты верхнего строения пути. Расчеты пути на прочность. Классификация рельсов по длине. Расчеты бесстыкового пути, страница 10

                                                  (1.25)

Р_ст – статическое давление колеса на рельс;

           – среднее дополнительное давление от колебаний рессор в расчетном сечении, кПа.

3.2.2 Определение силы Р_р и S_p

Сила Р_р является следствием колебаний подрессоренных масс на рессоры

Р_р=Z_max·Ж                                                     (1.26)

где     Z_max – f(v) и определяется по соответствующим эмпирическим формулам.

Для ВЛ-8, ВЛ-23 Z_max=10,9+9, 6·10^-4v² (мм).

Z_max представляет динамический прогиб рессор сверх статического.

Ж – жесткость рессор, отнесенная к одному колесу, кгс/мм.

Для нового подвижного состава

Р_р=(Р_ст-q)к_д                                                  (1.27)

к_д – коэффициент вертикальной динамики, определяемый по эмпирической формуле:

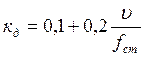,                                               (1.28)

где    f_ст – суммарный статический прогиб рессоры первой ступени и второй.

Максимально возможные перемещения Z_max у пассажирских вагонов при v=100 км/ч составляют 20мм, а при большей скорости – 25мм. Для большинства типов подвижного состава Z_max растет со скоростью

Z_max=а_рес+b_ресv²,                                             (1.29)

Для ВЛ-23, ВЛ-22^м, Вл-60Д, ВЛ-8

Z_max=10, 9+9, 6·10^-4v²,                                       (1.30)

Для ТЭП60, ТЭП10, ТЭ10, 2ТЭ10Л, ТЭ-30, ТЭ7, ТЭ-3, ТЭМ1

Z_max=7, 9+8, 0·10^-4v²,                                        (1.31)

Для других тепловозов и электровозов Z_max=15мм.

Обработкой большого числа экспериментов установлено, что  средняя величина дополнительного упругого прогиба рессор составляет 0,75 Z_max, а следовательно и средняя величина дополнительного вертикального давления от колебания рессор

,                                               (1.32)

Исследованиями установлено, что разница между средним  и максимальным значением силы Р_р составляет 3 среднеквадратических отклонения:

, отсюда

,                                                      (1.33)

3.2.3 Определение Р_нп и S_нп

Неровности пути имеют самую разнообразную форму (Холодецким приложена треугольная, Тимошенко – синусоидальную, Крачковский - параболическую форму). Наиболее неблагоприятной является синусоидальная форма, которая дает наиболее простые формулы, а реальные формы неровностей учитываются введением в расчетную  формулу специального коэффициента.

В расчетах приходится учитывать не только неровности пути в ненагруженном состоянии, но и так называемые динамические неровности, образующиеся под нагрузкой и являющиеся следствием неравноупругости рельсового основания по его протяжению. Динамический уклон определяется по формуле:

,                                                     (1.34)

где    А – коэффициент пропорциональности;

β – коэффициент, оценивающий влияние типа рельсов;

γ – коэффициент, оценивающий влияние рода балласта;

Р – давление колес на рельс;

l – расстояние между осями шпал.

Значение максимального дополнительного инерционного усилия Р_нп при расчете пути на деревянных шпалах определяется по приближенной формуле:

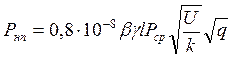                                      (1.35)

где    0,8 – коэффициент, учитывающий усредненную форму неровности;

β – для Р50 равен 1,0, для Р65 и Р75 – соответственно 0,85;

γ – для асбеста и щебеночного балласта равен 1,0;

Р_ср – средняя нагрузка на колесо;

q – неподрессоренный вес, приходящийся на одно колесо, кгс;

v – скорость движения, км/ч;

U – модуль упругости рельсового основания кгс/см².

Колебания вертикально давления колеса на рельс за пределами неровности, где они имеют наибольшее значение, подчинены закону:

                                        Р_нп=(Р_нп)_max sinφ

где    (Р_нп)_max – наибольшее значение Р_нп ;

φ – фаза колебаний.

При этом среднеквадратическое отклонение составляет 0,707(Р_нп)_max.

Следовательно, при расчете пути на деревянных шпалах

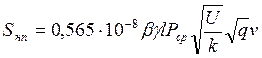                                           (1.36)

После перехода к системе СИ эта формула примет вид

,

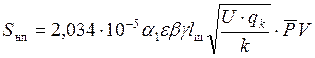где α1	-	коэффициент, учитывающий величину колеблющейся массы пути (деревянные шпалы – 1, а железобетонные – 0,931);
ε	-	коэффициент учета жесткости пути (деревянные шпалы – 1, а железобетонные – 0,322);
β	-	коэффициент, зависящий от типа рельсов (для рельсов Р50, Р65 и Р75 он равен соответственно 1; 0,87; 0,82)
γ	-	коэффициент учета рода балласта (щебень, асбест, сортированный гравий – 1; карьерный гравий, ракушка – 1,1, песок – 1,5);
lш	-	расстояние между осями шпал (при эпюрах укладки 2000, 1840 и 1600 шт/км lш соответственно 0,5 м; 0,55 м; 0,63).

3.2.4 Определение Р_инк и S_инк

Изолированные неровности на колесе встречаются довольно редко. При движении колес с изолированной неплавной неровностью на поверхности катания  - ползуном, выбоиной – получается удар, оказывающий очень большое дополнительной воздействие на рельс. Такие удары могут вызвать даже изломы рельсов, особенно зимой. Форма изолированной неровности принимается синусоидальной, а колесо прокатывается по рельсу, не отрываясь от него.

По ПТЭ на поверхности катания локомотивных колес ЭР и ДР с роликовыми буксовыми подшипниками глубина выбоины допускается не более 0,7мм, с подшипниками скольжение - ≤1,0мм, а вагонных колес с роликовыми буксовыми подшипниками - ≤1,0, с подшипниками скольжения - ≤2,0мм. С учетом быстрого закатывания краев неровностей, в расчет вводят глубину изолированной неровности колеса 2/3 первоначальной, т.е. соответственно 0,067см и 0,133см. Длина закатанной выбоины колеблется от 20см до длины окружности катания колеса.

При одном обороте колеса теория расчета сил инерции неподрессоренных масс с изолированной неровностью колеса совпала бы с теорией расчета тех же сил при движении колеса по плавной неровности на пути. Но катающееся колесо с неровностью, с незатухнувшими от нее свободными колебаниями в паре  “колесо-рельс”, наезжает на рельс следующей неисправностью и вызывает вынужденные колебания. Наложение указанных колебаний неопределенно.