Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров

1.Содержание ЦОС. Аналоговый, дискретный и цифровой сигналы.

Сигнал определяется как функция, которая переносит информацию о состоянии или поведении физической системы. Сигнал принимает форму электрических колебаний, которые зависят от времени и от пространственных координат. Математически сигнал представляется в виде функции одной или нескольких переменных. Различают три вида сигналов: аналоговый, дискретный и цифровой.

Если переменная t принимает дискретные значения, то сигнал называется дискретным.

t_к=k*∆t, k=0,1,2,…

X_д(t_k)=X_д(k*∆t)

Амплитуда отсчетов может быть тоже дискретной, т. е. принимать определенные уровни – кванты.

Каждый из уровней квантования представляется в виде двоичного кода. Цифровые отсчеты, представленные в виде кодов – это цифровой сигнал. Это изображение сигнала в виде цифр. Любая задача обработки сигналов – это извлечение и преобразование информации.

Успехи в развитие вычислительной техники и особенно появление микропроцессоров обусловили появление сложных алгоритмов обработки сигналов. Такие устройства работают не с реальным сигналом, а с его цифровым представлением. В общем виде процесс обработки такой:

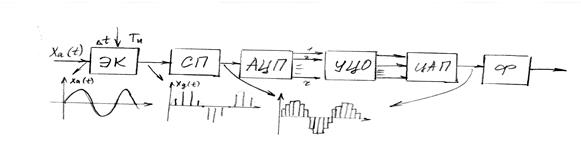
Аналоговый сигнал x(t) в сложной форме поступает на электронный ключ, который из аналогового сигнала формирует последовательность дискретных отсчетов с шагом по времени  t (дискретизация сигнала по времени).  Сигнал на выходе электронного ключа имеет вид последовательности коротких импульсов, промодулированных по амплитуде входным сигналом. Каждый сформированный отсчет в схеме памяти вытягивается на весь ∆t, это необходимо для аналогового – цифрового преобразования (АЦП). На выходе схемы памяти имеем  ступенчатое напряжение, амплитуда ступеньки равна амплитуде соответствующего отсчета сигнала. В АЦП ступеньки квантуются и превращаются в цифровой код. Весь аналоговый сигнал заменяется последовательностью чисел  N=T/ ∆t . Эта последовательность цифр поступает с АЦП в УЦО. УЦО – это вычислительное устройство, имеющее стандартную структуру. В УЦО над кодовыми словами производятся математические операции, соответствующие заданному алгоритму обработки сигнала. Устройство ЦОС может быть выполнено на основе жесткой и мягкой логики. Жесткая – каждая операция алгоритма выполняется отдельным блоком. Мягкая – все операции выполняются программно.

Схемы с жесткой логикой обладают большим быстродействием, но не позволяют корректировать или изменять алгоритм работы устройства. Схемы с мягкой логикой обладают меньшим быстродействием, но алгоритм работы  можно менять.

Если оконечное устройство цифровое – преобразований больше нет, если нет, то коды с помощью ЦАП преобразуются в аналоговый вид и фильтруются.

2.Аппроксимация в процессе синтеза рекурсивных дискретных фильтров

Расчеты рекурсивного дискретного фильтра имеют свои особенности. Все методы расчета  разделяют на три класса методов расчета передаточной функции рекурсивного дискретного фильтра.

1.Методы преобразования аналоговых фильтров в цифровые (метод билинейного преобразования, метод инвариантности импульсной характеристики, метод согласованного Z – преобразования).

2.Прямые методы расчета в Z – плоскости.

3.Методы, использующие алгоритмы оптимизации.

Метод билинейного преобразования (МБП).

Для расчета частотно-избирательных рекурсивных фильтров НЧ, ВЧ, полосовых и режекторных наиболее подходящим является метод билинейного преобразования функции T(S) фильтра прототипа в передаточную функцию H(Z) дискретного фильтра.

В этом методе используют следующие фильтры аналоговых фильтров прототипов:

1.фильтр Баттерворта с монотонно изменяющейся частотной характеристикой;

2.фильтр Чебышева с монотонно убывающей в полосе задержания и равномерной характеристикой в полосе пропускания;

3.фильтр, инверсный фильтру Чебышева

4.фильтр Золоторева - Кауэра – эллиптический

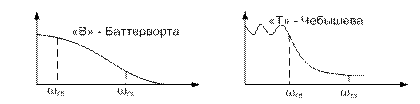
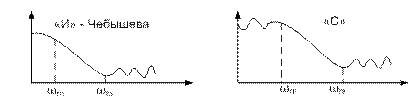
Такие фильтры подробно табулированы. Имеются справочники, в которых приводятся передаточные функции T(S), приводятся вид АЧХ и формулы, которые связывают граничные частоты фильтра с параметрами фильтра.

В методе билинейного преобразования в эту передаточную функцию подставляют вместо S функцию  f(Z):

S=f(Z) – зависит от того, какой фильтр проектируется