Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 3

Определение передаточной функции производится по этапам:

1)расчет нормированных цифровых граничных частот ;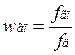

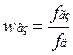
2) расчет параметра преобразования γ;

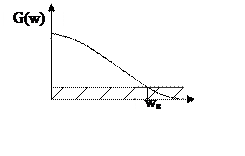
3)нахождение аналоговой граничной частоты w_к;

4) определение передаточной функции T(S) аналогового фильтра – прототипа (по справочникам);

5)определение передаточной функции H(Z) дискретного фильтра с помощью соответствующего билинейного преобразования;

6) контрольный расчет АЧХ фильтра.

Для ПФ и ЗФ исходные данные те же самые, только задаются 4 граничные частоты. Алгоритм определения H(Z) совпадает с указанным выше, но с дополнениями:

1) на втором этапе рассчитываются  γ и α;

2) на пятом этапе имеются особенности расчета. Полиномы T(S) первого порядка приводят после преобразования к полиномам второго порядка, а полиномы второго порядка порождают полиномы четвертого порядка по Z^-1. При получении окончательного выражения для H(Z) следует полиномы четвертого порядка разложить на множители в виде полиномов второго порядка. 

5. Принципы дискретизации сигналов. Модель непрерывного сигнала.

Непрерывный сигнал x(t) заменяется последовательностью его мгновенных значений x(t_k), которые называют отсчетами. Эти отсчеты взяты в определенные дискретные моменты времени t_k=k∆t, где ∆t – шаг или интервал дискретизации. При такой замене из рассмотрения исключаются все множество значений сигнала, находящихся внутри интервала ∆t.

Если ∆t=const, то дискретизация равномерная, если ∆t изменяется, то неравномерная (адаптивная). В основе математического описания дискретизации непрерывной функции лежит импульсная функция дискретизации:

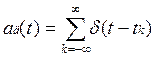. Тогда дискретизация непрерывной функции с математической точки зрения есть:

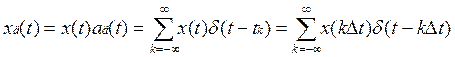
На практике реализация осуществляется с помощью ключевых схем:

При дискретизации по времени возникают задачи, связанные с выбором интервала ∆t. Первым этапом при определении ∆t является выбор модели сигнала.

Модель непрерывного сигнала.

В современных РТУ полезными, подлежащими обработке сигналами являются случайные функции времени (СП). Полное описание СП возможно с помощью многомерной плотности распределения. Известно 3 распределения:

1)гауссовское р.;

2)р. Дирихле;

3)р. Уишарта.

На практике разрабатывают модели сигналов, основанных на различных упрощениях и допущениях.

1) непрерывные реальные сигналы – нестационарные эргодические процессы.

Различают следующие виды СП:

а) СП с гауссовской плотностью распределения вероятности

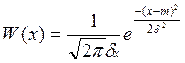
б) СП с равномерной плотностью распределения вероятности ; a≤x≤b

в) СП с распределением Рэлея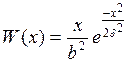

г) гармонический процесс с постоянной амплитудой и частотой, но со случайной фазой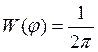

2) сигнал обычно характеризуется либо энергетическим спектром, либо корреляционной функцией.

- энергетический спектр

3) Вводятся ограничения на сигнал:

а) конечное значение средней мощности процесса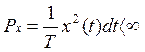

б) конечная шкала мгновенных значений

в) ограничение спектра сигнала по полосе

6.Сравнение методов реализации дискретных фильтров. Пример дискретного фильтра первого порядка.

Различают 3 группы методов реализации цифровых фильтров:

Метод свертки: основан на использовании импульсной характеристики фильтра.

y_n=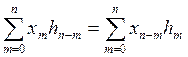.Применение этого метода возможно в том случае, если импульсной характеристике {h_n} является конечной во времени.

Метод рекурсии: на основе линейного разностного уравнения.

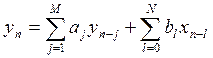- это выражение приводит к бесконечной во времени импульсной характеристике (БИХ фильтр).

Метод преобразования Фурье: основан на том, что ДПФ от свертки 2-х функций равно произведению ДПФ 1-й функции на комплексно сопряженное ДПФ другой функции. 

Преимущество нерекурсивных фильтров по сравнению с рекурсивными:

1) нерекурсивные фильтры могут иметь точно линейную ФЧХ;

2) мощность собственных шумов нерекурсивных фильтров гораздо меньше, чем рекурсивных;

3) для нерекурсивного фильтра проще вычисление коэффициентов, т.к. аппроксимирующая функция  линейно зависит от  коэффициентов С.

4)в системе с изменением частоты дискретизации применение нерекурсивных фильтров сокращает необходимое число арифметических операций.

Недостаток нерекурсивных фильтров по сравнению с рекурсивными: