Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 9

1)нельзя бесконечно увеличивать количество подинтервалов, их не может быть больше числа уровней квантования;

2)для малых значений плотностей вероятности относительная погрешность велика.

От недостатков дифференциального закона свободна оценка интегрального закона.

P{x_n≤ x_min+m∆x}=V_m/N,  V_m - количество точек выборки , попавших в интервал (x_min+m∆x)

P(x)

x

x min                                 x max

P(x_n< x_min)=0,  P(x_n ≤x_max)=1,   M_x=1-(x₁,x₂,..x_N)

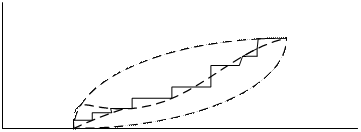
Для непрерывного сигнала при увеличении N, ступенчатая кривая превращается в непрерывную.

Для квантованного сигнала непрерывную линию получить нельзя. На этом графике наносят доверительный интервал. Чтобы вычислить доверительный интервал нужно знать закон распределения вероятности оценки. Если  при экспериментальных измерениях закон неизвестен, то количественной оценкой могут послужить мат. ожидание и дисперсия оценки.

23. Способы нумерации функций Уолша. Генерирование функций Уолша.

Способ нумерации называется упорядочиванием. Различают ФУ, упорядоченные по Уолшу, Адамару и Пэли. В любом из этих способов количество функций остается неизменным N=2ⁿ и отличаются они только правилом определения степеней функций Родемахера. Также используется способ, основанный на матрице Адамара. Матрица Адамара – квадратичная матрица порядка N→H_N такая, что . Все эти матрицы можно вычислять рекуррентным способом:

    ;  

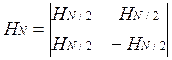
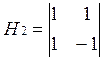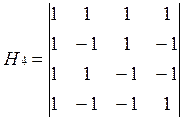
Используя эти матрицы функции Адамара определяют так: ФА определяется последовательностью прямоугольных импульсов, длительность которых 1/N, амплитуда равна 1, а полярность соответствует элементу матрицы Адамара.

На практике используется ограниченное число базисных функций, при этом при разложении в ряд только часть коэффициентов отлично от 0, поэтому стараются выбирать такой способ нумерации ФУ, который обеспечивает монотонное уменьшение коэффициентов фильтра. Это необходимо, чтобы уменьшить объем хранимой и передаваемой информации.

Генерирование ФУ

Это необходимо при восстановлении сигналов, т.к. каждый алгоритм восстановления можно представить в виде устройства. Работа схемы основана на первоначальной формуле:

n=3, ГМ – генератор меандра

 

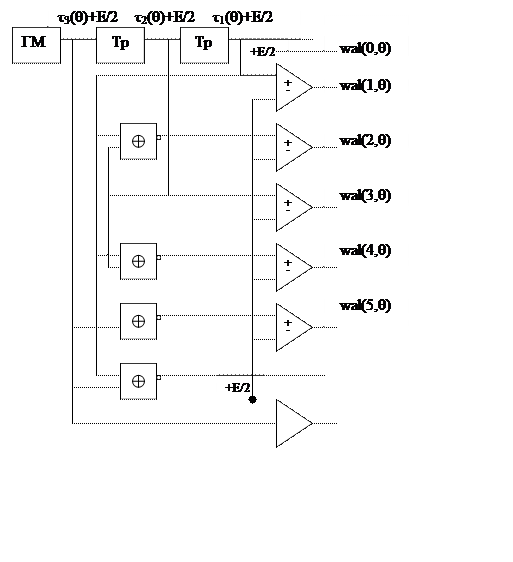
Все функции смещены вверх по уровню на E/2. Указанные функции Родемахера соответствуют смещенным ФУ 1,3 и 7 порядка. Смещение их вниз на E/2 осуществляется с помощью операционных усилителей. Остальные ФУ получаются с помощью сумматора по модулю 2 с инверсией.

Таблица истинности.

x	0	1	1	0
y	0	1	0	1
вых	1	1	0	0

Выходной результат получается обратным смещением.

24.Параметрический метод оценки законов распределения. Аппроксимация экспериментальных распределений.

Плотность распределения в виде гистограммы представляет мало ценности. В подавляющем большинстве случаев необходимо найти аналитическую запись. Для решения этой задачи можно воспользоваться несколькими методами:

1)воспользоваться своим предшествующим опытом и интуицией. Для этого строят гистограмму.

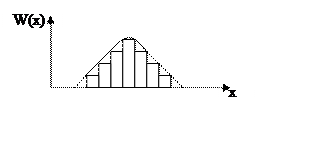
По виду кривой, используя опыт, говорят о том, какое это распределение.

2) Выбор типа распределения на основе изучения гистограммы и физических природных явлений.

3) метод моментов. Он позволяет формализовать процедуру подбора распределений и автоматизировать процедуру анализа. Этот метод учитывает тот факт, полное описание свойств СП можно выполнить, используя многомерный закон распределения, а можно задать все бесконечное множество моментов.

; 

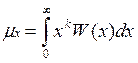Оказывается, что достаточно хорошо описать форму закона распределения, используя только 4 первые моменты: μ=m_x, M₂=δ_x², M₃, M₄. Для характеристики формы распределения используется величины.

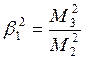- коэффициент асимметрии

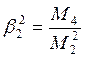-коэффициент эксцесса

Построим график

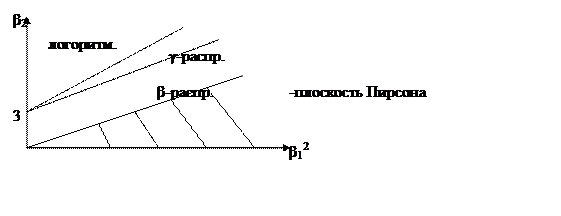
Каждому набору коэффициентов соответствует определенный закон распределения.

Метод моментов для определения типов законов распределения заключается в том, что по исходному массиву отсчетов объемом N определятся оценки моментов.

 ;

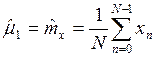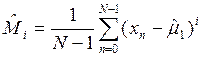
Затем находят оценки , наносятся на плоскость Пирсона и по положению этой точки можно определить закон распределения. После этого необходимо определить параметры закона распределения. Для этого используют либо метод максимального правдоподобия, либо метод моментов.