Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 5

Эти формулы позволяют анализировать влияние погрешности коэффициентов на положение полюсов.

В общем случае, этот эффект можно сгладить, если соответствующим образом выбирать способ реализации фильтров. Рекомендуется выполнять реализацию фильтров большого порядка в виде каскадного или параллельного включения фильтров первого и второго порядка.

9. Квантование непрерывных сигналов. Преобразование сигналов в цифровую форму.

Квантование непрерывных сигналов.

Суть квантования по уровню заключается в замене множества значений непрерывного сигнала дискретным конечным множеством заранее установленных значений. При этом непрерывная шкала мгновенных значений сигнала размером x_max заменяется дискретной шкалой, содержащей N_кв значений (уровней). Деления этой шкалы называются уровнями квантования. Интервал между уровнями называется – шаг квантования: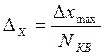

При этом квантование может быть равномерным или неравномерным. Если Δx=const– равномерное квантование. Если Δx≠const - то неравномерное.

Квантование заключается в том, что мгновенному значению сигнала ставится в соответствие уровень квантования. Это производится 3-мя способами:

1) Ближайший снизу.

2) Ближайший сверху

3) Округление

x

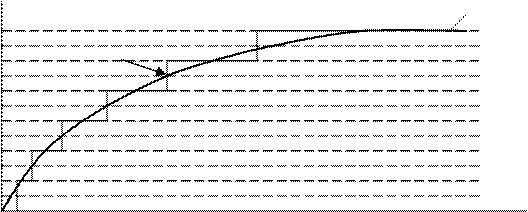                                                                                             X(t)

Xкв(t)

t 

                                                                                                                            

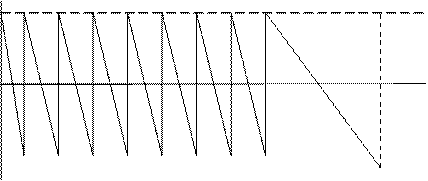
Шум квантования                                                                                                                                    

-

Основная характеристика этого шума – дисперсия: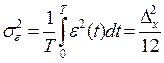

 - мощность шума

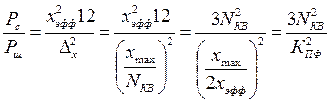
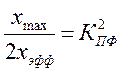 - пик фактор.

Отношение с/ш при квантовании определяется числом уровней квантования и статистикой (пик фактор).

Преобразование дискретизированных сигналов в цифровую форму.

Нужно заменить отсчеты их цифровым изображением в виде чисел в определенной системе счисления. n – основание, r – разряд.

  - общее число элементов кода.

Стараются эту величину минимизировать, т.е. найти оптимальную систему счисления.

;

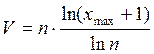
Нужно найти экстремум по n:

 ;    

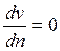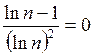
 => n=e

n	2	2.72	3	4	8	10	12
V/Vopt	1.06	1	1.006	1.06	1.42	1.58	1.77

Для представления в цифровом виде сигналов двоичная система используется, т.к. она  близка к оптимальной и просто реализуются элементы.

10. Пример дискретного фильтра второго порядка.

Разностное уравнение фильтра:

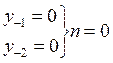
Передаточная функция может быть записана на основе выражения:

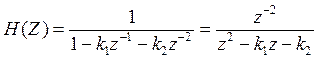; имеет 2 полюса и 2 нуля.

Корни этого уравнения: ;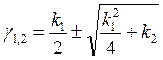

если  подобрать коэффициенты так, чтобы, 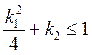то корни получаются комплексно-сопряженными:, .

Свойство корней уравнения:

;

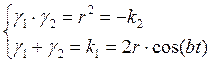Подадим на фильтр один дельта-импульс, тогда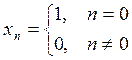

В результате вычислений получаем:

;

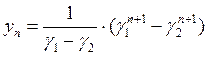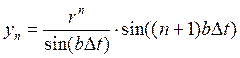- отсчеты затухающей амплитуды.

.

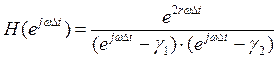Реализация фильтра:

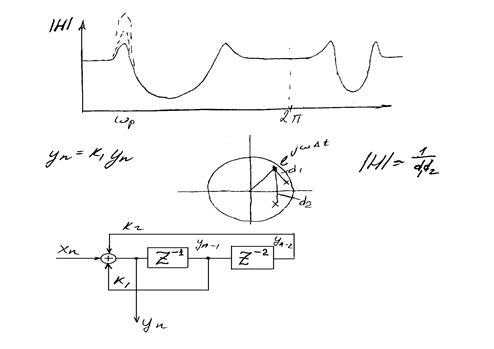
11. Дискретное преобразование Фурье. Свойства ДПФ.

В современной радиотехнике большое количество задач решается в частотной области. Необходимо из сигнала вычислить спектр.

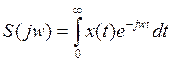
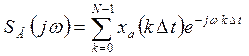
Рис. 1. Непрерывный сигнал и соответствующий ему спектр

Рис. 2. Дискретизированный сигнал и его спектр

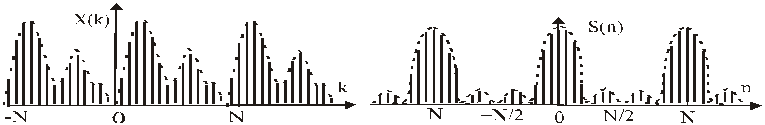
Рис. 3. Дискретный спектр и соответствующий ему сигнал

;

- прямое ДПФ

 - обратное ДПФ

Свойства ДПФ:

1.Свойство периодичности: ДПФ формирует периодический спектр, а ОДПФ – периодический сигнал.

2.Свойство симметрии: при четном N и действительном 

В частности, при  , т.е.  - действительное число. - тоже действительное число, т.к. .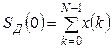

3.Свойство линейности:

4.Сдвиг

,

Если (умножить) смещать спектр по фазе, то появляется сдвиг сигнала по времени.

12. Эффекты квантования в цифровых фильтрах. Ошибки, вызываемые аналого-цифровым преобразованием.

Эти эффекты возникают тогда, когда реальные цифровые фильтры имеют дискретные параметры и на них поступают квантованные отсчеты сигналов. Различают 3 эффекта:

1) введение квантованных коэффициентов фильтра приводит к нелинейным соотношениям. Эти соотношения трудно, а иногда невозможно решить точно.

2)квантование входных сигналов приводит к возникновению шума квантования. Этот шум проходит через фильтр и изменяет его характеристики.