3)квантование или округление результатов умножений. Влияние округления на фильтр зависит от того, как осуществляется округление и от конкретной реализации фильтра. Если ошибки округления не зависят друг от друга, то получаем модель, в которой к различным точкам цепи подключаются различные источники шума.
Ошибки, вызываемые аналого-цифровым преобразованием.
Ошибки,
вызываемые квантованием сигнала, можно считать некоррелированными, если при
переходе от одного отсчета к другому м.б. пройдено несколько уровней
квантования. Для каждого из этих отсчетов шум квантования 
. Если пренебречь другими ошибками, можно
вычислить дисперсию шума на выходе фильтра. Сигнал и шум независимы и поэтому
мы можем рассмотреть прохождение сигнала и шума через фильтр независимо. Фильтр
считаем либо передаточной функцией H(Z)
или импульсной характеристикой {hn}. Если
импульсная характеристика, то отсчеты шума на выходе: 
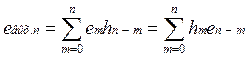
em – отсчеты шума квантования входного сигнала, они независимы.
Дисперсия шума на выходе равна: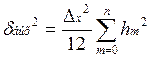
. При этом предполагается, что до момента m=0 шума не было. Тогда можно сказать, что шум на выходе
зависит от времени и от n.
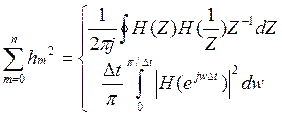
13. Особенности практического использования ДПФ.
При использовании ДПФ часто возникают 3 проблемы, из-за которых могут быть сделаны неверные выводы:
1)Появление ложных спектральных составляющих.
2)Размывание спектральных составляющих.
3)Паразитная амплитудная модуляция спектра.
Рассмотрим отдельно:
1)Возникает в том случае, если неправильно выбрана верхняя частота.
Это явление,
при котором ВЧ-ые компоненты сигнала могут быть приняты за НЧ-ые. Причина:
недостаточная частота дискретизации. Вывод: необходимо правильно выбирать 
. 2)Это явление всегда имеет место.
Причина – ограниченный объем обрабатываемых данных (конечная выборка).
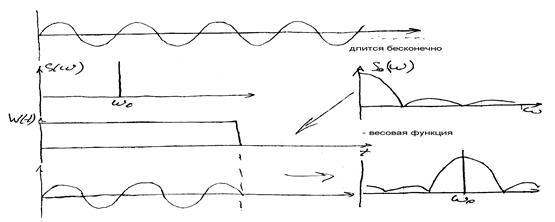
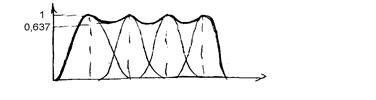
С этим явлением необходимо бороться. Исключить его полностью не удается, однако уменьшить боковые лепестки удается. Для этого используют весовые функции.
Подавление лепестков зависит от используемой весовой функции. Этих весовых функций существует много.
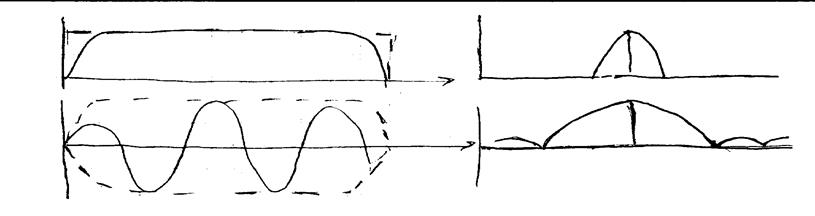
3)Она возникает в том случае, когда по отдельным дискретным отсчетам спектра пытаемся вычислить его значение на других частотах между этими дискретами.
Это связано с тем, что каждый коэффициент Фурье получается пропусканием сигнала через фильтры.
Используется подход, когда преобразуемый массив отсчета сигнала дополняется нулевыми отсчетами.
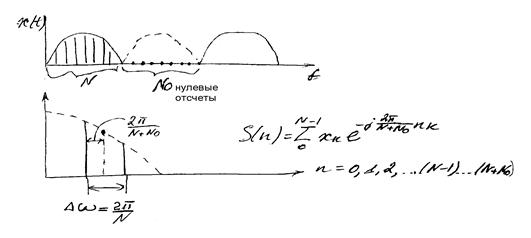
Позволяет вычислить промежуточные отсчеты.
Алгоритм ДПФ – хороший алгоритм, но у него есть недостаток: большие затраты времени и памяти при вычислении спектра.
14.Анализ шумов в цифровом фильтре первого порядка.
yn=kyn-1+xn ; 
; 
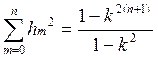
Если n→∞,
то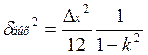 
По этой формуле можем определить уровень шумов на выходе. Эта величина зависит от шага квантования. Величина этого шума тесно связана с числом разрядов выходного регистра.
Рассмотрим конкретный случай. k=0.99. Тогда δ2вых=4∆х2; δвых=2∆х – СКО. Чтобы определить число разрядов выходного регистра, необходимо учитывать минимально допустимое отношение с/ш и динамический диапазон полезного сигнала. Пусть шум 40дб, амплитуда сигнала должна в 100 раз превышать СКО шума → разрядность регистра = 200∆. Сам сигнал имеет динамический диапазон 40дб → чтобы записать максимальный сигнал нужно еще в 100 раз увеличить число разрядов = 20000∆.
Из формулы для дисперсии шума видно, что мощность определяется коэффициентом k.
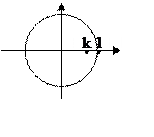
k=1-ε ; →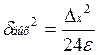 
Мощность шума обратно пропорциональна расстоянию от полюса до единичной окружности.
15. Быстрое преобразование Фурье (БПФ).
Основная идея этого алгоритма заключается в том, что мы многократно расчленяем исходную выборку на несколько более коротких выборок и выполняем все вычисления с более короткими выборками, а затем по ним, используя свойство линейности, находим спектр исходной последовательности. БПФ – это тоже дискретное преобразование, только организованное специальным образом.
Рассмотрим реализацию алгоритма:
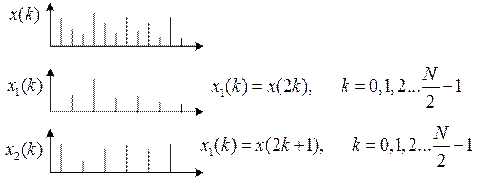
Запишем ДПФ:
; 
; 
.
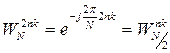Вычисление спектров:
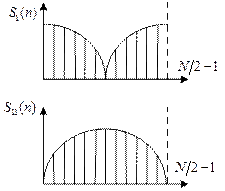
На основе свойства линейности:
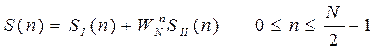
- во второй половине.
Эти формулы лежат в основе БПФ, т.е. когда по спектрам полученных массивов получаем спектр результирующего сигнала.
Обычно их изображают в виде направленного графа:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.