1)при одинаковом требовании к АЧХ, отсутствии требований к ФЧХ и постоянной частоте дискретизации нерекурсивные фильтры требуют выполнения большего числа операций.
2)вариант на основе ДПФ м.б. использован для реализации как рекурсивного, так и нерекурсивного фильтра. Используется тогда, когда порядок фильтра очень большой. При большом порядке первые два способа приводят либо к сложным схемам, либо к длительным вычислениям. Преимущество метода на основе ДПФ сказывается при порядке 28-30.
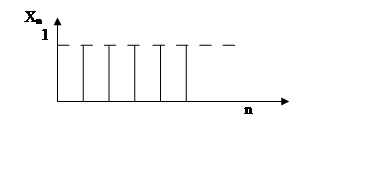
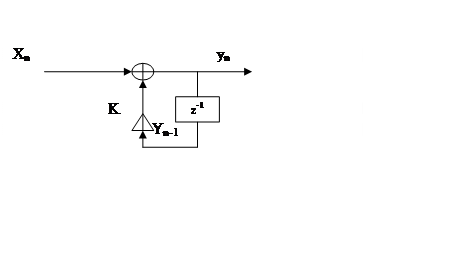
Пример цифрового фильтра первого порядка.
![]() в этом уравнении чтобы фильтр был
устойчив, нужно |k|<1. Решение этого уравнения:
в этом уравнении чтобы фильтр был
устойчив, нужно |k|<1. Решение этого уравнения: 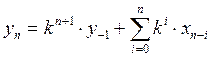 ; y-1
– начальные условия, напряжение на выходе фильтра при n=0.
; y-1
– начальные условия, напряжение на выходе фильтра при n=0.
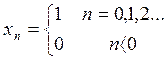
Для этого сигнала xn решение будет: 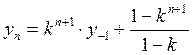 ; если
|k|<1, то при n ®¥ получаем:
; если
|k|<1, то при n ®¥ получаем:
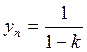 ;
;
![]()
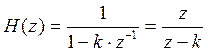
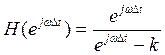
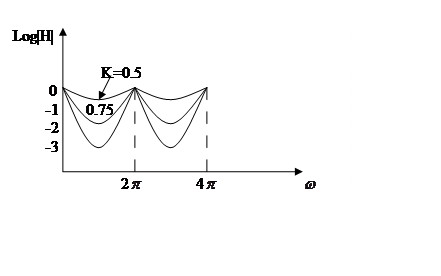
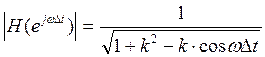
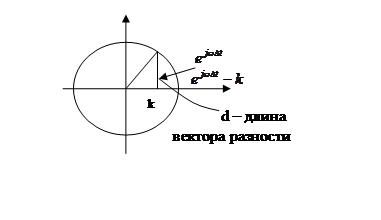 |H|=
|H|=![]() ;
;
7. Предельная дискретизация сигналов с ограниченным спектром.
Наиболее завершенной предельной дискретизацией является дискретизация на основе теоремы Котельникова. В соответствии с этой теоремой мы можем восстановить сигнал по дискретным отсчетам по формуле:
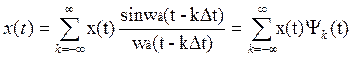
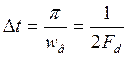 ; wв- верхняя частота в спектре сигнала
; wв- верхняя частота в спектре сигнала
Если сигнал конечной длительности, то можно взять только N = T/∆t отсчетов:
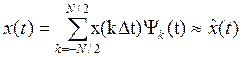

![]() -погрешность
-погрешность
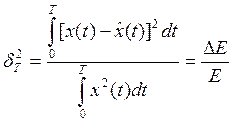 ;
; ![]() - общая погрешность
- общая погрешность
Это не корректная модель.
Всегда, когда делается дискретизация возникает вопрос восстановления. Восстановление на практике производится двумя способами: фильтрационным и интерполяционным.
Фильтрационный способ основан на теореме Котельникова.
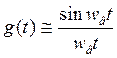 . Фильтр
с такой импульсной характеристикой должен иметь частотную характеристику в виде
прямоугольника. Но реально это получить не возможно. Возникают ошибки.
. Фильтр
с такой импульсной характеристикой должен иметь частотную характеристику в виде
прямоугольника. Но реально это получить не возможно. Возникают ошибки.
В интерполяционном методе нужно сгенерировать N функций:
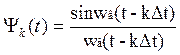 и
просуммировать. Важно правильно выбрать wв.
и
просуммировать. Важно правильно выбрать wв.
Всегда, когда делают преобразование аналогового сигнала в цифровую форму, ставят фильтр.

В связи с этими особенностями восстановление по Котельникову на практике не используется. Основная ценность этой теоремы в том, что она доказывает принципиальную возможность восстановления сигнала. Она справедлива только для детерминированных сигналов. Для случайных процессов теорема справедлива в том случае, если спектр сигнала равномерен и ограничен.
На практике чаще всего используются интерполяционные многочлены. Наиболее распространенный многочлен Ла – Гранжа:
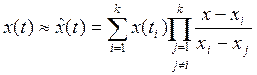
К – порядок многочлена; чем больше к, тем больше отсчетов используется для восстановления. Наиболее распространены интерполяции 0, 1 и 2 порядков.
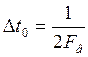 ;
;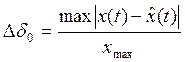 - приведенная погрешность
- приведенная погрешность
Для того, чтобы правильно выбрать частоту дискретизации в соответствии с формулами, необходимо:
-задается или определяется допустимая погрешность, определяется верхняя частота сигнала;
-по верхней частоте находят допустимый интервал дискретизации;
-выбирают вид интерполяции;
-рассчитывают требуемый шаг дискретизации.
8. Эффекты квантования в цифровых фильтрах. Постановка задачи. Ошибки, вызываемые неточными значениями постоянных параметров.
Эти эффекты возникают тогда, когда реальные цифровые фильтры имеют дискретные параметры и на них поступают квантованные отсчеты сигналов. Различают 3 эффекта:
1) введение квантованных коэффициентов фильтра приводит к нелинейным соотношениям. Эти соотношения трудно, а иногда невозможно решить точно.
2)квантование входных сигналов приводит к возникновению шума квантования. Этот шум проходит через фильтр и изменяет его характеристики.
3)квантование или округление результатов умножений. Влияние округления на фильтр зависит от того, как осуществляется округление и от конкретной реализации фильтра. Если ошибки округления не зависят друг от друга, то получаем модель, в которой к различным точкам цепи подключаются различные источники шума.
Ошибки, вызываемые неточными значениями коэффициентов фильтра.
yn=k1yn-1+k2yn-2+xn. Полюса этого уравнения комплексные.
![]() ;
; 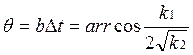
Ошибки в определении коэффициентов приводят к ошибкам в определении полюсов. Произведение b∆t означает, что при одной и той же ошибке, уменьшение интервала дискретизации увеличивает погрешность определения резонансной частоты b. Требуются применение более высокой точности вычислений. Если ∆k1 и ∆k2 – малы и независимы, то
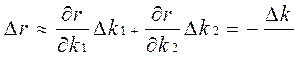 ;
; 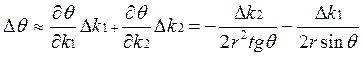
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.