Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 8

В основе лежит теорема свертки. Спектр свертки 2х сигналов равен произведению спектров этих сигналов.

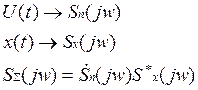
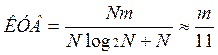- коэффициент ускорения вычислений, N=1024

Если вычислять автокорреляционную функцию

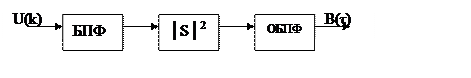
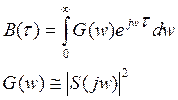
20. Цифровая обработка случайных сигналов. Оценка моментов.

С обработкой случайных сигналов приходится иметь дело практически в любой радиотехнической системе. Обработка таких сигналов производится с разными целями. Часто задачами обработки случайных сигналов является оценка различных характеристик случайного сигнала: математического ожидания, дисперсии, корреляционной функции, закона распределения, спектральной мощности. В любом случае исходным является массив х₁,х₂,….х_N, где N-объем выборки.

Оценка мат. ожидания.

Рассматривается стационарный, эргодический случайный процесс.

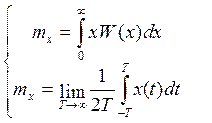
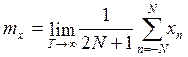
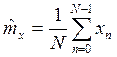- оценка мат. ожидания

Любая оценка имеет какие-то свойства, выраженные в количественном виде. Эти свойства позволяют сравнивать между собой разные оценки.

, то оценка называется несмещенной.

Дисперсия оценки: 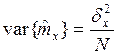- оценка мат. ожидания является состоятельной (справедлива для гауссовского случайного процесса.)

Для получения оценки наилучшим считается метод максимального правдоподобия. Этот метод основан на анализе многомерного закона распределения: . Находят такое , при котором закон принимает максимальное значение: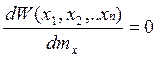

Решают это уравнение и находят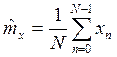

Оценка дисперсии.

Для дисперсии: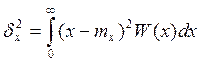  

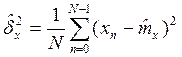
Найдем мат. ожидание этой оценки: 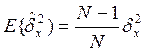- оценка смещенная.

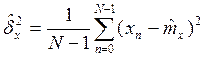- используют для оценки дисперсии.

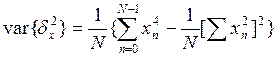
Оценка состоятельная.

21. Краткие сведения о функциях Уолша. Свойства функций Уолша.

Существуют различные способы задания ФУ. Наиболее часто используются способы задания их через другие функции – функции Родемахера:

Эта функция принимает значение ±1. Функции Родемахера ортонормированны:

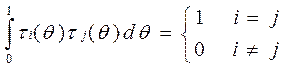
Но они несимметричны и через них вводят ФУ, свободные от этих недостатков.

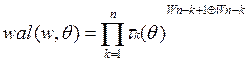; W - порядок ФУ

w_i – i-тый разряд номера W в двоичной системе счисления

W=6, n=3 , 

Эти вычисления можно представить в виде таблицы.

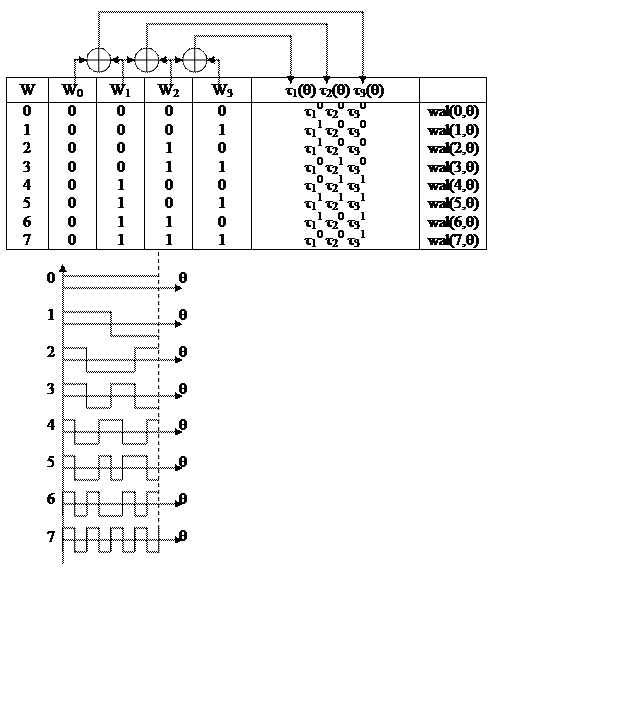
Свойства функций Уолша:

1) функция ортонормированна на интервале от 0 до 1:

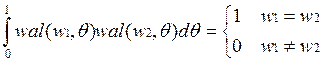
2) свойство мультипликативности: перемножение ФУ дает ФУ:

3) ФУ могут служить ортогональным базисом для негармонического спектрального представления сигналов.

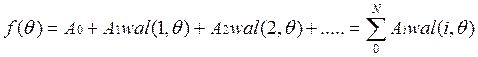
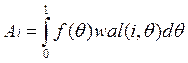
22. Непараметрические методы оценки законов распределения.

Непараметрический подход используется в том случае, когда нет, и не может быть каких-либо предположений о классе закона распределения. Закон распределения непрерывный и отличен от 0 во всем диапазоне изменения сигнала. Методы: гистограммный , метод Парзена, метод разложения по базисной функции, метод полиномов Смирнова, метод К ближайших соседей.

Наиболее простой-метод гистограмм. Алгоритм:

1)область возможного существования признаков разбивается на подобласти: ∆_l- многомерный случай; ∆x_l- многомерный случай

2)подсчитывается число наблюдений, которое попало в каждую подобласть;

3)вычисляется оценка:

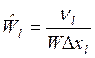 -одномерное;  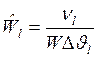- многомерное

4)строится график:

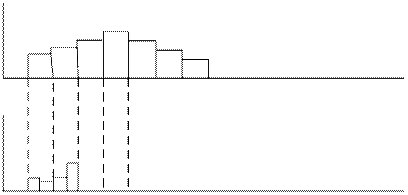
Оценка дифференциального закона называется гистограммой.

∑ W_l∆x_l=1

Количество интервалов и их ширина существенно влияют на вид этого закона. На практике  количество интервалов:  8-10.

Достоинства гистограмм: простота оценки и явный физический смысл. Недостаток: при увеличении N до бесконечности и неизменном количестве подинтервалов оценка сводится не к точному закону распределения:

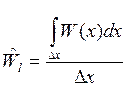
Эта оценка несостоятельная. Чтобы это обойти, необходимо при неограниченном объеме выборки ограничить количество подинтервалов и уменьшить их.

Необходимо:

1. lim ∆V=0

N→∞ 

2. lim V_l = ∞ 

N→∞ 

3. lim V_l/N=0

N→∞ 

1)обеспечивает сходимость пространственно усредненной величины к точному значению при однородном сокращении подобластей и непрерывном законе распределения.

2)выполняется, если во всем диапазоне существования признаков закон распределения не равен 0.

3)необходимо для обеспечения сходимости.

2 способа выполнения этих условий:

а) сжатие начальных подобластей так, чтобы ширина их (объем) была: ∆V_l~1/√N                Это метод  окна Парзена.

б) метод k ближайших соседей.

При цифровой обработке сигналов есть особенность при построение гистограмм: