25. Дискретные функции Уолша. Свойства дискретных функций Уолша.
Для цифровых методов спектрального анализа и обработки сигналов наибольший интерес представляют дискретные ФУ. Эти функции являются отсчетами непрерывных ФУ. Каждый отсчет расположен в середине связанного с ним элемента непрерывной ФУ. Если всего N элементов, то длительность будет 1/N.
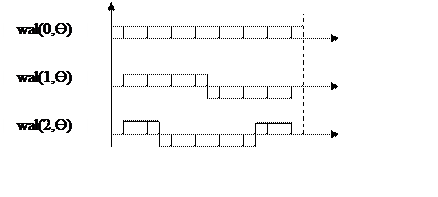
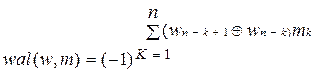
mk – к-ый разряд номера отсчета ФУ, Wi=0,1, mk=0,1
Другой формой представления ФУ является матрица Адамара. Номера строк этой матрицы соответствуют номерам функций, а номера столбцов – номерам отсчетов.
Свойства дискретных ФУ:
1) ортогональность
![]()
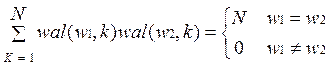 , где N – норма
этих функций
, где N – норма
этих функций
2) мультипликативность
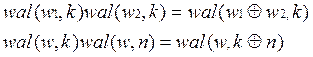
3) ортогональность позволяет использовать их для разложения в ортогональном базисе.
x(t) – сигнал, xk – отсчеты, N
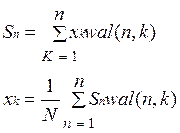 -
прямое и обратное преобразование Уолша
-
прямое и обратное преобразование Уолша
Эти преобразование обладают свойством периодичности Sn=Sn+mN, m=0,1,2…
4) связано с теоремой запаздывания:
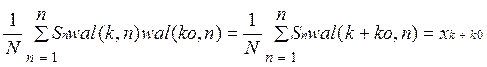
26. Цели и классификация методов цифрового спектрального анализа.
Основной целью спектрального анализа является оценивание спектральной плотности мощности (СПМ) процесса и обнаружение факта присутствия в течение определенного интервала времени периодического сигнала (процесса) и оценка параметров этого сигнала (амплитуды, фазы, частоты). Обработка сигнала производится последовательно во времени, но при этом одновременно обрабатывается массив из N отсчетов.
Тн=N∆t; Тн – интервал наблюдения, ∆t – длина реализации.
Можно выделить 2 группы методов цифрового спектрального анализа:
1) методы, которые в той или иной форме реализуют Фурье анализ дискрет-го процесса.
2)методы, в которых априорно выбирается линейная модель, представляющая собой дискретный фильтр, и определяются параметры этой модели, которые обеспечивают на выходе фильтра процесс максимально близкий к исходному (который анализируется). Тогда по параметрам этой модели можно получить все интересующие сведения.
К первой группе методов относятся корреляционный метод (Блекмена-Тьюке), метод коррелограмм и метод периодограмм.
Ко второй группе относятся методы оценивания спектральной плотности мощности на основе авторегрессии скользящего среднего, метод Прони, метод Писаренко.
27.Линейные дискретные и цифровые фильтры. Краткие сведения о Z -преобразовании.
Дискретным фильтром называется устройство, которое реализует следующий алгоритм:
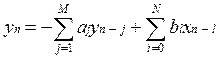 , где xn
– n-ные отсчеты входного сигнала фильтра, которые
следуют с интервалом ∆t; yn – отсчеты выходного сигнала фильтра; aj и bi – коэффициенты фильтра. С математической точки зрения
это выражение представляет собой разностное уравнение. Если aj и bi зависят только от текущего индекса, т.е. являются
функциями времени, но не зависят от величин x и y, то фильтр называется линейным дискретным фильтром, а
уравнение – линейным разностным уравнением. Если aj и bi просто постоянные числа, то фильтр называется
инвариантным по времени.
, где xn
– n-ные отсчеты входного сигнала фильтра, которые
следуют с интервалом ∆t; yn – отсчеты выходного сигнала фильтра; aj и bi – коэффициенты фильтра. С математической точки зрения
это выражение представляет собой разностное уравнение. Если aj и bi зависят только от текущего индекса, т.е. являются
функциями времени, но не зависят от величин x и y, то фильтр называется линейным дискретным фильтром, а
уравнение – линейным разностным уравнением. Если aj и bi просто постоянные числа, то фильтр называется
инвариантным по времени.
Из уравнения видно, чтобы найти отсчеты выходного сигнала, надо выполнить 3 операции: задержку сигналов, умножение и суммирование. Все это, возможно, выполнить только в цифровом виде. Цифровое устройство, которое это реализует, называется цифровым фильтром. В цифровом фильтре входные и выходные сигналы являются цифровыми.
Существуют 2 класса цифровых фильтров: рекурсивные и нерекурсивные.
Если ни один из коэффициентов aj≠0, то фильтр рекурсивный. Если все aj=0, то нерекурсивный. Рекурсивный фильтр – устройство с обратной связью и бесконечной импульсной характеристикой. Нерекурсивный фильтр – фильтр с конечной импульсной характеристикой.
Краткие сведения о Z-преобразовании.
Z-преобразование:
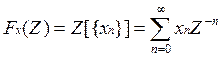 , где Z –
комплексное число, Z=ejw∆t.
, где Z –
комплексное число, Z=ejw∆t.
Свойства Z-преобразования:
1) линейность
fn(1)→F1(Z)
fn(2)→F2(Z) , то Z[a fn(1)+b fn(2)]=a F1(Z)+b F2(Z)
2) преобразование удовлетворяет теореме сдвига
fn(1); fn(2)=fn-m(1)
F2(Z) =Z-m F1(Z); F1(Z)=Z[{fn(1)}]
Существует обратное Z-преобразование, когда по известному Z-образу находится решетчатая функция fn(1)= Z-1 [F1(Z)].
F(Z)=f0+f1Z-1+f2Z-2…..
28. Оценка спектра мощности методом периодограмм.
Рассмотрим преобразование Фурье оценки автокорреляции:
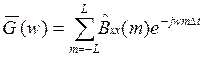 ;
; 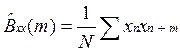
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.