Оценка корреляции является состоятельной, но ее преобразование Фурье является оценкой несостоятельной (т.е. при увеличении N, дисперсия не стремится к 0). Расчет оценки СПМ довольно сложен и в законченном виде возможен лишь в некоторых частных случаях.
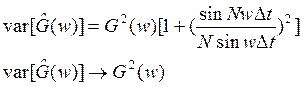
При этом если N увеличивается, то вычисляются новые отсчеты функции.
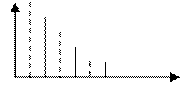
Свойство несостоятельности затрудняет практическое использование СПМ, однако, простота получения оценки с помощью БПФ позволяет улучшить характеристики. Чтобы улучшить оценки можно использовать сглаживание.
Метод периодограмм состоит из 2х этапов:
1) весь интервал разбивается несколько подинтервалов с целью получения оценки;
2)усреднение результатов, получившихся на нескольких интервалах наблюдения с целью уменьшения дисперсии.
Необходимо так организовать наблюдения, чтобы оценки на разных интервалах были независимы.
29. Передаточные функции дискретных фильтров. Временные и частотные характеристики дискретных фильтров.
Передаточная функция – отношение реакции цепи к воздействию.
H(Z)=Y(Z)/X(Z)
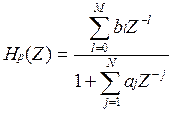 -передаточная функция рекурсивного
фильтра
-передаточная функция рекурсивного
фильтра
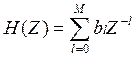 - передаточная функция
нерекурсивного фильтра
- передаточная функция
нерекурсивного фильтра
Эти функции как и в аналоговых цепях облегчают анализ структурной схемы фильтра.
Временные характеристики.
Важнейшей временной характеристикой фильтра является импульсная характеристика.
{hn}- реакция фильтра на воздействие в виде дельта-функции.
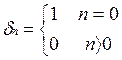
Рассматривается при нулевых начальных условиях. Между импульсной характеристикой и передаточной функцией существует математическая связь.
Y(Z)=H(Z)X(Z)
Z[{hn}]=H(Z)
Z-преобразование импульсной характеристики совпадает с передаточной функцией.
{hn}=Z-1[H(Z)]
Частотные характеристики
Эти комплексные частотные характеристики получают путем подстановки в изображение передаточной функции H(Z) Z=ejw∆t.
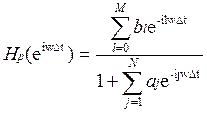 -для рекурсивного фильтра
-для рекурсивного фильтра
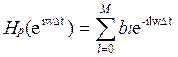 -для нерекурсивного фильтра
-для нерекурсивного фильтра
Из этих выражений можно найти АЧХ и ФЧХ фильтра по обычным правилам нахождения модуля и фазы комплексного числа.
A(w)= │H(eiw∆t)│; φ(w)=arg[H(eiw∆t)]
Частотные характеристики дискретных фильтров имеют 2 важных свойства:
1) Z=ejw∆t – периодическая функция. Тогда частотные характеристики тоже являются периодическими функциями.
2) Для цифровых фильтров с вещественными коэффициентами АЧХ – четная функция частоты, а ФЧХ – нечетная функция частоты.
30. Сглаживание спектральных оценок. Основные свойства оконных функций.
Возможны 3 варианта действий:
1) усреднение независимых оценок.
Весь объем N разбивается: N=kM; находится оценка Gl(n) для каждого массива объемом М.
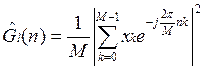 ; l=1,2,…k
; l=1,2,…k
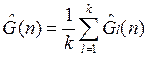 - усредненный
спектр
- усредненный
спектр
Дисперсия 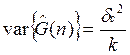 ,
при условии, что у каждой из оценок одинаковая дисперсия. Если k→∞, то дисперсия → 0. Получается состоятельная оценка.
,
при условии, что у каждой из оценок одинаковая дисперсия. Если k→∞, то дисперсия → 0. Получается состоятельная оценка.
2) заключается в том, что сглаживание производится путем свертки с некоторым спектральным окном.
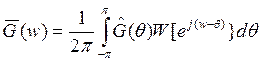
Свертка эквивалентна перемножению отсчетов ковариационной функции на окна во временной области.
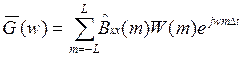

3) является компромиссным между 1) и 2): N также разбивается на k отрезков, для каждого из них применяется весовая обработка.
N=kM;
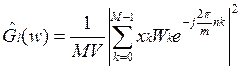 , где
, где 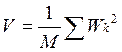 - нормирующий множитель
- нормирующий множитель
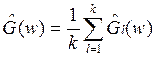
Основные свойства оконных функций:
Существует много параметров, которые количественно оценивают весовые функции и по которым осуществляют их выбор. Наиболее важные из них следующие:
1) эквивалентная шумовая полоса ∆FшN – полоса пропускания фильтра с прямоугольной частотной характеристикой, имеющей такое же максимальное усиление, как и оконная функция и накапливающей такой же шум.
2)ширина главного лепестка на уровне L - ∆FNL

3) соотношение 2х полос: 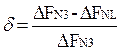 - характеризует эффективность оконной
функции в том случае, когда обрабатываемая последовательность отсчетов
представляет собой сумму гармонических сигналов с частотами некратными частотам
ПФ.
- характеризует эффективность оконной
функции в том случае, когда обрабатываемая последовательность отсчетов
представляет собой сумму гармонических сигналов с частотами некратными частотам
ПФ.
4) когерентное усиление оконных функций – эта величина характеризует усиление гармонического сигнала, частота которого совпадает с одной из базисных частот ДПФ.
5) максимальный уровень боковых лепестков спектра Фурье оконной функции и асимптотическая скорость спадания боковых лепестков при увеличении частоты.
6) паразитная АМ.
31. Структурные схемы дискретных фильтров.
Широко используются 2 формы изображения структурной схемы фильтра: прямая форма и каноническая форма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.