Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 13

35. Кодирование чисел в цифровых фильтрах. Особенности проектирования цифровых фильтров.

Кодирование

Этот вопрос возникает в случае, когда фильтр реализуется аппаратным способом. Известно, что в цифровых устройствах для представления используются прямой, обратный и дополнительный коды. При выборе между обратным и дополнительным кодом необходимо учитывать 2 фактора:

1) заключается в том, что у обратного кода существует 2 нулевых значения:+0 и -0;

2)наличие у обратного кода циклического переноса при сложении кодов.

При реализации операции алгебраического сложения обычно используется дополнительный код, а при реализации умножения – прямой код. Поэтому в устройствах, реализующих цифровую фильтрацию, необходимо делать преобразователи кодов.

Важным является вопрос масштабирования чисел при реализации вычислений. В цифровых устройствах наиболее распространены 2 формы записи чисел: с фиксированной запятой и с плавающей запятой. Однако, чаще используется комбинированный вариант масштабирования, который позволяет получить простую схему и обеспечить высокую точность.

Особенности проектирования фильтров

Проектирование фильтров заключается в определении требований к частотной и импульсной характеристике и нахождении условий, которые обеспечат эти требования. Однако, указанная цель не определяет параметры фильтра однозначно. Поэтому задаются дополнительные условия, которые позволяют оптимизировать параметры фильтра в соответствии с каким-либо критерием. Различают 2 критерия: критерий минимизации необходимого количества ячеек памяти и минимизации необходимого числа алгебраических операций.

Вся задача проектирования разделена на 3 этапа:

1) аппроксимация заданных характеристик фильтра; определение алгоритма его работы и определение импульсной характеристике и передаточной функции.

2) выбор разрядности квантованных данных

3) определение необходимой вычислительной производительности по заданным условиям и алгоритму обработки.

Методы аппроксимации специфичны для рекурсивного и нерекурсивного фильтров.

36. Определение параметров АР-модели по анализируемым данным.

Обычно при спектральном анализе значение автокорреляционной функции неизвестно. Определение параметров АР-модели выполняют, имея лишь отсчеты x_n. Сложность зависит от соотношения отсчетов и порядка модели. Для однократного вычисления используют различные методы линейного предсказания (вперед, назад и совместное).

Для линейного предсказания вперед (автокорреляционный метод):

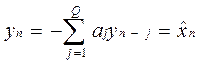- оценка отсчета

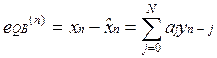- ошибка линейного предсказания

В этом методе минимизируется общая ошибка предсказания: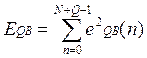

При использовании этого метода в сумме n принимает значения от 0 до , N+Q-1. При этом считается, что за пределами n=0,….,N-1;    x_n=0. Тогда

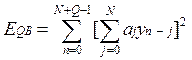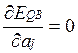; , j=1,2,..,Q

Эта система линейных алгебраических уравнений. Выполняется 2 этапа: 1) вычисляются коэффициенты системы; 2)решается система уравнений: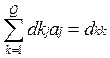

После того, как система уравнений решена, нужно найти дисперсию входного шума: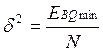

Алгоритм Берга (линейное предсказание вперед-назад):

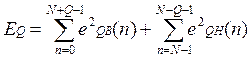
Дифференцируем эту величину по коэффициентам a_j и находим параметры модели.

37.Разновидности нерекурсивных фильтров и требования к ним.

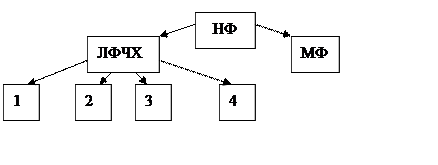
ЛФЧХ (с линейной фазочастотной характеристикой) делятся на 4 вида и различаются способом записи частотной характеристики:

1) N – нечетная, b_l=b_N-i-l, коэффициент симметричный;

2) N – четная, b_l=b_N-i-l, коэффициент симметричный;

3) N – нечетная, b_l=-b_N-i-l, коэффициент антисимметричный;

4) N – четная, b_l=-b_N-i-l, коэффициент антисимметричный.

Основное свойство передаточной функции фильтров заключается в том, что передаточную функцию можно представить в виде произведения 3х передаточных функций:

H_лфчх(Z)=H₁(Z)H₂(Z)H₃(Z)

При этом ее свойства таковы, что: . Отличается тем, что нули H₁(Z) совпадают с нулями общей функции H(Z), расположенным внутри единичной окружности или лежащим на единичной окружности. При этом они имеют четную кратность. Нули H₁(Z) совпадают с нулями H(Z), расположенных вне единичной окружности.

;

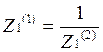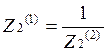
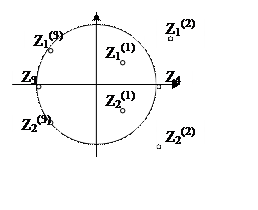
Передаточная функция  H₃(Z)=const или ее нули совпадают с нулями исходной передаточной функции, расположенных на единичной окружности и имеющих нечетную кратность.