Аналоговый, дискретный и цифровой сигналы. Основная функция сигнала. Аппроксимация в процессе синтеза рекурсивных дискретных фильтров, страница 7

Рассмотрим массив из 8-ми исходных чисел:

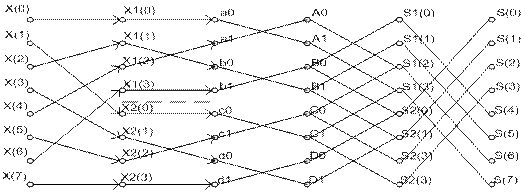
На каждой ступени N/2 – умножений, а всего таких ступеней .

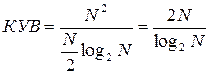
- коэффициент ускорения вычислений

16. Анализ шумов в цифровом резонаторе.

y_n=k₁y_n-1+k₂y_n-2+x_n;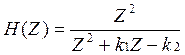 

; 

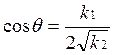
Чтобы найти сумму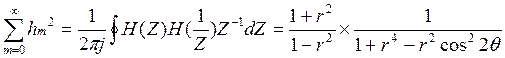

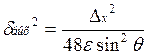
Мощность шума обратно пропорциональна расстоянию до единичной окружности, но она еще зависит от углового положения полюса, чем меньше Ө, тем больше уровень шума. Это означает, что фильтры с низкой резонансной частотой требуют больше двоичных разрядов.

17. Разновидности БПФ.

Существует много вариантов БПФ. Каждый из них позволяет получить дополнительный выигрыш в скорости вычисления для конкретной ситуации, но все они основаны на идеи проведения вычислений не с N-точечным ДПФ, а вычисление нескольких ДПФ меньшей размерности. Различаются способом разделения на мелкие части. Самый простой вариант, когда размеры массива представляют через целую степень 2. Разновидности: с прореживанием по времени и по частоте.

Алгоритм с прореживанием по времени: исходные данные разделяются на четную и нечетную последовательности. Алгоритм с прореживанием по частоте: исходную последовательность делят пополам, и затем вычисляют по ним четные и нечетные отсчеты спектра.

 

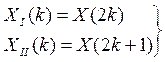
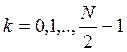
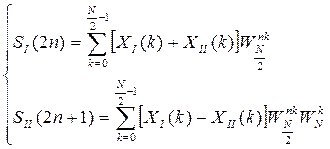
Исходная последовательность делится многократно, пока не дойдем до 2-х точечных массивов. Затем вычисляются промежуточные спектры.

Алгоритм для произвольного .

Разделяют массив: в одном  чисел, в другом .

   ;

   ;         

Окончательное выражение для спектра (n и k подставляем в формулы) 

  

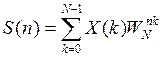
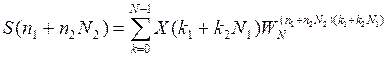
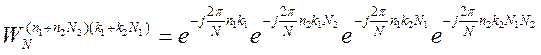
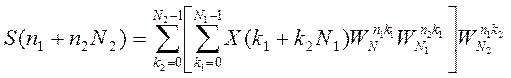
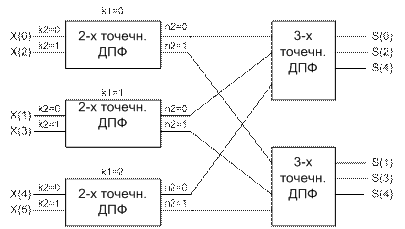
Кроме того, может быть БПФ с произвольным основанием, но чаще с основанием 2,4,16. Существуют еще некоторые специфические алгоритмы.

18. Ошибки цифрового фильтра, вызванные квантованием произведений. Эффект «мертвой» зоны.

Возникает при округлении результатов вычислений отсчетов сигнала и коэффициентов фильтра при каждом умножении, т.е. на сигнал накладывается последовательность шумовых отсчетов. Эффект подобен шуму квантования, но точка, в которую вводится шум, зависит от конкретной схемы фильтра.

1)Прямая форма реализации фильтра:

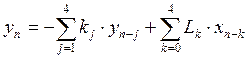
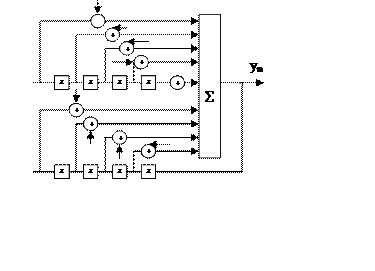
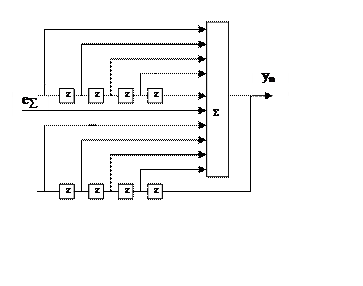       Шумы независимы и все попадают в сумматор, поэтому можно нарисовать эквивалентную схему.

; ;

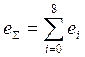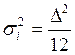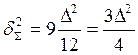
Избежать этого шума можно, если число регистров сумматора увеличить. Точность расчетов при этом увеличится, но заметно увеличится время вычислений.

2)Каноническая форма реализации этого фильтра:

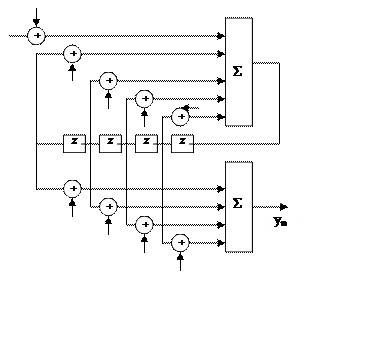
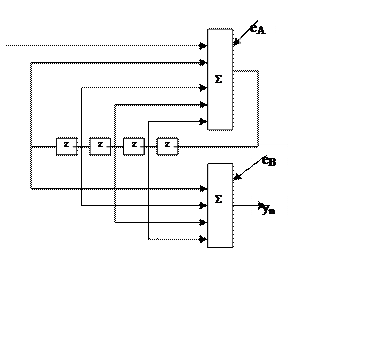
Эквивалентная схема.

; ; ;

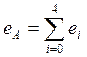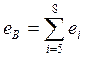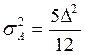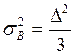
Прямая форма вводит больше шума, т.к. там шум проходит через часть схемы, которая соответствует полюсам в полосе прозрачности. В канонической схеме и через полюсы и через нули с малым усилением.

H(Z)=R(Z)*1/P(Z), R(Z)-часть функции, соответствующая нулям; P(Z)-часть функции, соответствующая полюсам.

Дисперсия шума записывается через интеграл:

Прямая форма: 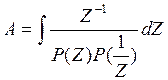; каноническая форма: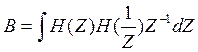

Эффект «мертвой» зоны.

Ошибки, вносимые каждым округлением, не всегда взаимно-некоррелированны.

; k=0.96 ; x_n=10; y_n-1=265

n	0	1	2	3	……	nT
До округления	264,4	263,44	262,42	261,52		261,62
После округления	264	263	262	262		262

Если сделать точные вычисления, то установившимся значением будет 250.

y_n-1=245

n	0	1	……	nT
До округления	245,2	245,2		245,2
После округления	245	245		245

Любое значение в этой области будет установившимся - эффект «мертвой» зоны.

Даже, если сигнал на выходе фильтра станет равен 0, то значения не упадет до 0, а останется прежним. Возможны возникновения стационарных колебаний.

19. Вычисление корреляционного интеграла на основе БПФ.

Во многих РТУ необходимо вычислять следующий функционал: 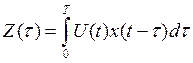-интеграл свертки, где

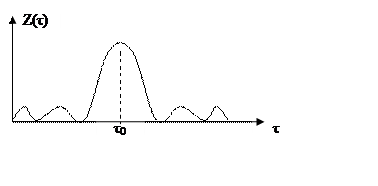
Если в этой формуле шум будет отсутствовать, то получим автокорреляционную функцию.

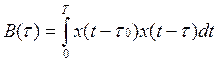
Если записать в дискретном виде, то 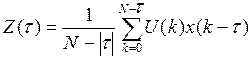, τ=0,±1,…,±m

По этой формуле производится приблизительно mN операций. Чтобы ускорить вычисления используют БПФ.

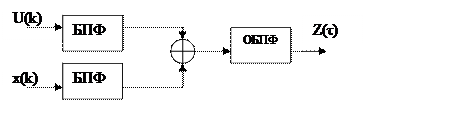
Выполняется Nlog₂N+N операций.