Основные определения и положения химической термодинамики. Взаимосвязь между основными законами, страница 22

На практике удобнее пользоваться уравнениями, записанными для приращений функций.  Чтобы перейти, например к уравнению, выражающему приращение энергии Гиббса, запишем уравнение (2.67) для двух состояний системы, т.е. для G₁  и G₂.  Потом из уравнения для конечного состояния вычтем уравнение для начального состояния.  Итоговое соотношение  для приращений G и H . будет иметь вид:

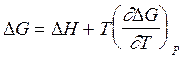                                       (2.68)

Уравнения Гиббса -Гельмгольца часто используют, заменяя термодинамическую функцию работой, т.е.

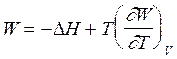                                      (2.69)

Соотношения между физико-химическими свойствами

системы и термодинамическими параметрами

Термодинамические функции по сути  их вывода можно рассматривать как эквиваленты полезной работы, которую  выполняет система в конкретных условиях опытов. С учетом этого,  а также того, что они являются характеристическими функциями, т.е. позволяют вывести любые термодинамические уравнения, термодинамические функции применяют для связывания различных, определяемых экспериментально, физико - химических свойств системы с термодинамическими параметрами. Полученные соотношения используются в практических расчетах.

Среди химических свойств можно назвать такие как: растворимость вещества, электрические характеристики и др. Например, работу гальванического элемента (W_э) часто представляют выражением  . Здесь e- физико-химическая характеристика, напряжение гальванического  элемента,  равное предельному значению разности электродных потенциалов элемента  () при токе, стремящемся к нулю. Вместе с тем,  работа при постоянных давлении и температуре связана с энергией Гиббса соотношением: W_э = - D G.  Отсюда вытекает связь энергии Гиббса с напряжением гальванического элемента:   - D G = nFe.

Химическийпотенциал

Ранее речь шла главным образом  о процессах, при которых количество вещества не изменялось. Между тем, в результате любой химической реакции эти изменения происходят.   Оценивать такие изменения удобно с помощью понятия о химических потенциалах.

Пусть протекает реакция, которую можно представить стехиометрическим уравнением:

a₁A₁ + a₂A₂ +¼ + a_nA_n = b₁B₁ + b₂B₂ + ¼ + b_nB_n                                (2.70)

Число молей вещества, входящих в систему переменно. При этом  внутренняя энергия системы меняется.

В общем случае величина любой термодинамической функции зависит от параметров состояния реакционной системы, т.е. от p, V, Tиn_i. Например,  значение энергии Гиббса меняется не только с изменением величин pи T , но и от изменения количества любого реагента. Поэтому можно записать:

G = f(p, T, n_A1¼n_An, n_B1¼n_Bn)                                 (2.71)

Изменение энергии Гиббса с учетом выражения (2.71) будет иметь вид:

           (2.72)

Здесь индексы при частных производных  n(A, B) показывают постоянство концентраций  любых веществ (А, В). Индексыn(A_j, B_j) указывают на постоянство концентраций любых веществ (А, В), кроме  веществ   (A_j, B_j). Частные производные по отдельным реагентам представляют собой вклад в общее изменение энергии Гиббса связанное с изменением  в ходе реакции количества данного реагента.  Эти производные обозначают символом  m и называют  химическим потенциалом вещества i.

  В терминах   m и с учетом уравнений (2.57), (2.66) последнее выражение  можно представить следующим образом:

dG = Vdp - SdT + Sm_i dn_i                                       (2.73)

Несложно показать, что член Sm_i dn_i войдет в аналогичные соотношения  для полных дифференциалов других термодинамических функций.

dU = TdS - pdV +Sm_i dn_i

                                         dH = TdS +Vdp + Sm_i dn_i                                                    (2.74)

dA = -pdV - SdT + Sm_i dn_i