Основные определения и положения химической термодинамики. Взаимосвязь между основными законами, страница 21

Если работа процесса равна 0, то такой процесс считается равновесным. Например, изотермически равновесный процесс без затраты внешних сил может протекать самопроизвольно только в направлении убывания энергии Гиббса до достижения минимума, после чего изменения потенциала оказываются невозможными,  иначе говоря равными нулю. Этому минимуму отвечает термодинамически равновесное состояние системы.

Аналогичный анализ можно выполнить и относительно других термодинамических функций (см. табл. 2.7).

Использование  термодинамических функций для

 построения математического аппарата термодинамики

Как видно из схемы, показывающей взаимосвязи между основными законами и принципами равновесной термодинамики, понятийный аппарат термодинамики основан на использовании законов и принципов термодинамики, а математический аппарат представлен уравнениями, связывающими термодинамические функции и их производные с физико- химическими свойствами и между собой. В связи с таким использованием термодинамических функций их часто называют характеристическими функциями[25].

Следует отметить, что большинство термодинамических формул самостоятельного значения не имеют. Они предназначены для решения очень узкой проблемы, а именно: для связывания конкретных функций через термодинамические параметры.  Поэтому в термодинамике существует множество формул. Методика их вывода достаточно проста.  Почти все они получаются применением двух простых математических теорем: теоремы о произведении частных производных и теоремы о приравнивании накрест взятых производных[26].

Примером образования термодинамических формул с использованием термодинамических функций и их производных может служить вывод уравнений Гиббса - Гельмгольца.

Эти уравнения позволяют избежать использование в явном виде зависимостей термодинамических функций (G, A) от энтропии, выступающей в качестве  независимой  переменной.

Рассмотрим вывод уравнения для условий p = const, T = const.

В этом случае по определению имеем:

 G = U + pV - TS                                                  (2.61)

Выведем полный дифференциал функции G.

dG = dU + pdV - TdS + Vdp - SdT                                           (2.62)

На основании уравнения (2.56) при условии, что dW’= 0 можно записать:

TdS = dU + pdV                       (2.63)

Сочетая уравнения (2.62) и (2.63) получаем:

dG = Vdp - SdT                                           (2.64)

Из математики известно, что полный дифференциал любой функции может быть выражен с помощью частных производных этой функции по соответствующим переменным. Поэтому, рассматривая в качестве независимых переменных Т и р, для функциональной зависимости вида   G= f(T,p) нетрудно вывести выражение:

                                     (2.65)

Сравнивая уравнения (2.64) и (2.65) можно получить, что:

        и 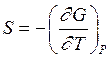                                   (2.66)

Из уравнений (2.66) следует, что термодинамические параметры и функции можно представлять в виде частных производных[27].

Подставим выражение для энтропии (2.66) в уравнение (2.57). В результате получаем уравнение Гиббса –Гельмгольца для энергии Гиббса:

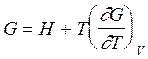                                                                      (2.67)

На основе формул- определений вида (2.59 а) и (2.60 а), а также соответствующих производных для других термодинамических функций  можно получить уравнения семейства уравнений Гиббса –Гельмгольца для любых функций.